_
Detalhes esquecidos em Oblivion
Não posso ainda, pelo desagradável que é tornar-se um spoiler, de tratar algumas coisas de Oblivion (2013, IMDB, Wiki). Já nos primeiros minutos de filme ficamos sabendo que uma civilização alienígena atacou a Terra inicialmente explodindo a Lua, e com isso causando tsunamis colossais que arrasaram nossa civilização.
Não posso ainda, pelo desagradável que é tornar-se um spoiler, de tratar algumas coisas de Oblivion (2013, IMDB, Wiki). Já nos primeiros minutos de filme ficamos sabendo que uma civilização alienígena atacou a Terra inicialmente explodindo a Lua, e com isso causando tsunamis colossais que arrasaram nossa civilização.
O problema é que o que causariam os tsunamis seriam marés, e estas realmente são causadas pela Lua (e não somente por ela, pois o Sol também tem uma pequena influência), mas não por ela estar íntegra ou em pedaços, mas sim pela sua massa total, seja em que agregação for.
O que interessa predominantemente, portanto, é a posição do centro de massa da Lua em relação à Terra. Noutras palavras, a distância deste, mais uma certa contribuição da distribuição das massas dos pedaços - se a Lua fosse feita em pedaços - em relação às massas de águas na Terra.
Primeiramente, trataremos da distância do centro de massa da Lua e como ele pode, mesmo com a explosão desta, ficar no mesmo lugar em que está.
Primeiramente, façamos um modelo simplificadíssimo da Lua, como um disco, evidentemente plano, que parta-se em “fatias” com a explosão. A seguir, separemos estas fatias por uma distância que seria o impulso dado a cada fatia pela explosão e calculemos, dois a dois, os centros de massa aproximados de cada par de “fatias”, depois, dos centros de cada par, dois a dois até chegarmos a um único centro de massa de todo o conjunto, o que aqui, considerarei, com certa coragem, de chamar simpaticamente de “método do móbile”.
Primeiramente, trataremos da distância do centro de massa da Lua e como ele pode, mesmo com a explosão desta, ficar no mesmo lugar em que está.
Primeiramente, façamos um modelo simplificadíssimo da Lua, como um disco, evidentemente plano, que parta-se em “fatias” com a explosão. A seguir, separemos estas fatias por uma distância que seria o impulso dado a cada fatia pela explosão e calculemos, dois a dois, os centros de massa aproximados de cada par de “fatias”, depois, dos centros de cada par, dois a dois até chegarmos a um único centro de massa de todo o conjunto, o que aqui, considerarei, com certa coragem, de chamar simpaticamente de “método do móbile”.
Recomendo a leitura na Wikipédia:
Evidente que a Lua não é um disco, e sua divisão são resulta em algo parecido com uma pizza mal cortada, mas a questão tridimensionalmente seria a mesma. Alerto que o esboço acima e o adiante teve o tratamento no “olhômetro”, pois as medidas e valores, em si, aqui, não interessam, e sim o raciocínio envolvido. Igualmente as proporções e distâncias foram negligenciadas.
Agora percebamos que com a distribuição da massa da Lua em seus pedaços, isto em coisa alguma altera a posição de tal centro de massas da Terra.
Assim, se a civilização alienígena desejasse realmente causar marés colossais, deveria mudar a posição do centro de massa da Lua em relação à Terra, por exemplo, com uma colossal explosão no seu lado oculto ou em certo ângulo favorável, arremessando-a para uma posição mais próxima da Terra.
No esboço acima, foi representada apenas a deformação das massas de água de um lado do planeta, pois as marés, na verdade, sempre tem uma simétrica do lado oposto.

Setas pretas: Força gravitacional devido à Lua. Setas brancas: Força diferencial "de balanço/líquida" relativa ao centro da Terra, correspondente à força de elevação das marés. - Editado de www.jodcast.net.
Observemos que no passado a Lua estava mais perto da Terra e produzia marés imensas, sendo tal fato apontado como um dos mecanismos que propiciou a formação da vida. Isto é devido aos fatos ligados a cada vez mais sólida hipótese do “Big Splash”, da formação da Lua após o impacto da “proto-Terra” com um corpo aproximadamente do tamanho de Marte.
Após um período de agregação do material parcialmente ejetado na colisão, a massa da Lua consolidou-se aproximadamente com a massa que possui hoje. Variações pequenas por impactos posteriores serão aqui desprezados, pois tanto a Terra quanto a Lua receberam muito material nos bilhões de anos seguintes, com um taxa maior nas primeiras centenas de milhões de anos depois do grande impacto, pois o sistema solar estava ainda num período com muitos corpos errantes - aqui, no sentido de fora das órbitas harmoniosas que hoje observamos, restando apenas as poucas exceções que inclusive nos ameaçam.
Após um período de agregação do material parcialmente ejetado na colisão, a massa da Lua consolidou-se aproximadamente com a massa que possui hoje. Variações pequenas por impactos posteriores serão aqui desprezados, pois tanto a Terra quanto a Lua receberam muito material nos bilhões de anos seguintes, com um taxa maior nas primeiras centenas de milhões de anos depois do grande impacto, pois o sistema solar estava ainda num período com muitos corpos errantes - aqui, no sentido de fora das órbitas harmoniosas que hoje observamos, restando apenas as poucas exceções que inclusive nos ameaçam.
Desta posição próxima inicial, na medida que o momento angular da Terra está sendo gradualmente transferido para a dinâmica orbital da Lua, a faz recuar lentamente da Terra a uma taxa de aproximadamente 38 milímetros por ano. Em consonância com a conservação do momento angular, a rotação da Terra está diminuindo gradualmente, e o dia da Terra aumenta, assim, em cerca de 23 microssegundos por ano (excluindo os rebotes glaciais). Ambos estes valores são válidos apenas para a configuração atual dos continentes, e sendo-se mais detalhado ainda, quando soma-se a influência do geóide.
Recomendo e referência do acima:
Para entendimento do que seja o Big Splash: YouTube
Documentário The Universe - The Moon. (2007) - parte que mostra a hipótese Big Splash aos 39 minutos: YouTube
A simulação neste documentário apresentada: YouTube
Este mecanismo tem operado por 4,5 bilhões de anos, desde que os oceanos se formaram na Terra. Há evidências geológicas e paleontológicas que a Terra girou mais rápido e que a lua estava mais perto da Terra no passado remoto. O ritmo das marés tem alternado camadas de areia e outros depósitos em estuários com grandes fluxos de maré. Ciclos diários, mensais e sazonais podem ser encontrados nos depósitos.
Os ritmos das marés de 620 milhões de anos atrás mostram que ao longo de centenas de milhões de anos a Lua diminuiu a uma taxa média de 22 milímetros por ano e o dia prolongou-se a uma taxa média de 12 microssegundos por ano, ambos cerca de metade de seus valores atuais. Este registro geológico é consistente com essas condições de 620 milhões de anos atrás, com as evidências apontando para sendo o dia de então de 21,9 ± 0,4 horas, e havia 13,1 ± 0,1 meses sinódicos/ano e 400 ± 7 dias solares/ano. A duração do ano permaneceu praticamente inalterada durante este período, porque não existe evidência de que a constante da gravidade tenha mudado. A taxa média de recessão da Lua entre tal período e agora foi 2,17 ± 0,31 centímetros/ano, o que representa cerca de metade da taxa atual.
Nos primeiros anos - entenda-se aqui algumas centenas de milhões de anos - a Terra e a Lua passaram pelo “bombardeio intenso tardio” - hipótese cada vez mais consolidada, uma fase de agregação do sistema solar na qual colisões enormes ainda aconteciam, e não temos de nos preocupar num primeiro momento - novamente, um momento que seja de milhões de anos - com os oceanos de então, pois cada impacto de corpo de dezenas de quilômetros era capaz de volatilizar boa parte dos oceanos que por ventura existissem.
Recomendo e referência do acima:
Por fim, temos de tratar a distribuição dos pedaços da Lua em órbita e sua influência nas marés.
Como pode-se ver em quadro da animação de partículas modelando o impacto que num determinado período a “massa pré-Lua” estaria distribuída em órbita da Terra em recuperação do impacto.
Como pode-se ver em quadro da animação de partículas modelando o impacto que num determinado período a “massa pré-Lua” estaria distribuída em órbita da Terra em recuperação do impacto.
Que esta massa distribuída tem centro de massa, já demonstramos claramente, pois todo o corpo ou conjunto de corpos tem centro de massa. O que é interessante se entender aqui é que pegando-se apenas dois corpos, que mesmo posteriormente vão formar a Lua, percebe-se que estes, mesmo possuindo o óbvio centro de massa, produzirão atrações individuais que minimizarão uma maré “total”, e mostramos isso no esquema abaixo, completamente, novamente, no “olhômetro” e “em rabisco”, sejamos sinceros.
Conclusão: Uma maré maior é causada por uma massa mais concentrada, e não por um centro de massa definido.
Pode-se entender isso por outro caminho, quando pensa-se numa jornada por um “trem gravitacional”. Quanto mais profundo, mais massa está acima de sua cabeça (digamos) e também produz atração gravitacional, até que num centro perfeito do geoide terrestre (ou de qualquer corpo celeste) esta seria anulada, pois homogênea em todas as direções. Assim, a máxima atração gravitacional é a que se encontra na superfície, em posições onde a distância até o centro de gravidade do corpo em questão seja a mínima.
Para entender esta questão com muito mais detalhes: Surface gravity - Wikipédia {en}
Para entender esta questão com muito mais detalhes: Surface gravity - Wikipédia {en}
Como exemplo de um raciocínio completamente diverso no campo da ficção, a série Space: 1999 (1975-1977, IMDB, Wiki), apresenta a Lua saindo de sua órbita ao redor da Terra e vagando pelo espaço por causa de uma explosão num depósito de material radioativo.
Só aí teria diversos pontos para tratar de “liberdades poéticas”, digamos, nos temas envolvidos ao longo da série, mas o raciocínio do movimento seria correto.
Como exemplo no terreno da ficção também de efeitos desastrosos da mudança da posição da Lua até em relação à “marés de crosta”, o filme ‘A Máquina do Tempo’ (The Time Machine, 2002, IMDB) as aborda como mecanismo da tragédia que se abate sobre a humanidade a partir de determinao momento de seu futuro, e também por explosões na Lua (pretendendo inclusive a construção de campos de golfe!), embora naquele filme, a mudança de sua posição fique subentendida pelo seu diâmetro angular no céu.
Elysium, Tártaro da atmosfera
Tártaro é a personificação do Mundo Inferior. Nele estão as cavernas e grutas mais profundas e os cantos mais terríveis do reino de Hades, o mundo dos mortos, para onde todos os inimigos do Olimpo são enviados e onde são castigados por seus crimes. - Wikipédia
Não me aterei a tecer comentários extensivos sobre Elysium (IMDB). A imprensa especializada já os fez por inúmeros ângulos, no campo “ideológico”, como distopia, do quanto é inferior a Distrito 9 (www.imdb.com), etc. Apenas alertaria que tem-se de abandonar esta mania de obsessão por permanente melhoria, da sempre nova quase obra-prima, quando não é exigida uma após a outra de todo ator, diretor ou produtor, como se a indústria do cinema não desejasse apenas vender pipocas, e lá de vez em quando, produzir algo duradouro na cultura, quase por acaso, não por objetivo primordial.
Neill Blomkamp continua bom para danar junto com sua equipe na antecipação no tecnológico (seja no terrestre, seja no alienígena) e robôs andróides, exoesqueletos, armas e space shuttle apresentam uma verossimilhança impressionante.
A própria estação (se é que podemos chamá-la assim) Elysium é convincente… até chegarmos no que tratarei aqui.
Neill Blomkamp continua bom para danar junto com sua equipe na antecipação no tecnológico (seja no terrestre, seja no alienígena) e robôs andróides, exoesqueletos, armas e space shuttle apresentam uma verossimilhança impressionante.
A própria estação (se é que podemos chamá-la assim) Elysium é convincente… até chegarmos no que tratarei aqui.
Elysium simula a gravidade de seus ricos moradores com a centrifugação (com a pseudoforça centrífuga) , aos moldes do já mostrado em inúmeros filmes e num conceito já bem consolidado nos escritos de Konstantin Tsiolkovsky , já em 1903, e levado aos mais técnicos detalhes por Wernher von Braun e Willy Ley nos anos 50. Foi magnificamente realizado cinematograficamente em 2001 - Uma Odisseia no Espaço de Kubrick - tanto na estação orbital quanto na nave, Discovery One, rumo a Júpiter - e numa avaliação que faço, de maneira extremamente realista, na aparência, na aplicação, nos resultados e na escala, no filme que considero cientificamente realista até descambar para uma coisa desastrosa que é Missão: Marte (IMDB).
Até aí, tudo bem. Eu, riquíssimo naquele futuro distópico (para os outros) só perceberia realmente que não estou na superfície terrestre (ou num corpo celeste de gravidade semelhante) olhando o horizonte, percebendo que estou numa concavidade, pois pelo meu peso, produzindo uma aceleração “de escape” da rotação* equivalente aos aproximadamente 9,8m/s² que enfrento aqui em São Paulo, e sem variações significativas, enfrentaria em qualquer lugar da superfície terrestre, das mais altas montanhas ao mais profundo silo submarino (pois a sensação depende de estar-se ao ar ou gases equivalentes em densidade, e em pressões, digamos, “humanas”).
*Atentem por motivos didáticos para os termos e as aspas, após ler o artigo sobre a pseudoforça, pelo menos, na Wikipédia, linkado acima. Recomendo também ler a oposta desta “pseudoaceleração”, que seria, exatamente como a pseudoforça a ela relacionada, a aceleração centrípeta.
O mesmo poderíamos dizer se eu estivesse numa nave qualquer acelerando-se a 9,8m/s², e disto deriva muito dos raciocínios iniciais de Einstein sobre a gravidade.
Mas voltemos ao ar que eu respiraria ali.
O meu peso dependeria da aceleração “de escape”, esta da rotação, mas não a pressão da atmosfera!
Assim, as paredes de “cristal” de Elysium, mesmo sendo altíssimas como são representadas, não poderiam produzir uma coluna de ar que produzisse a pressão “humana”. O peso da atmosfera depende da gravidade e no caso, da pseudoforça centrífuga, mas a pressão, que é causada pelo peso sobre áreas em que o fluido atmosfera “incide”, exige um peso da coluna de ar.
Para calcular isso, poderíamos usar uma equação barométrica, mas nem necessitamos disso para mostrar que a situação ali é absurda, e façamos cálculo muito mais simples.
Digamos que aquelas paredes tivessem 2 km, e toda a atmosfera não tivesse um gradiente de pressão, o que é uma argumento forçado, pois sempre ao irmos em direção ao centro da estação em rotação, a pseudoforça reduz-se, exatamente pois a velocidade tangencial reduz-se, ainda que a angular mantenha-se obviamente mesma, e como vê-se na equação abaixo, a aceleração centrípeta diminui conforme o raio diminui.
Digamos que aquelas paredes tivessem 2 km, e toda a atmosfera não tivesse um gradiente de pressão, o que é uma argumento forçado, pois sempre ao irmos em direção ao centro da estação em rotação, a pseudoforça reduz-se, exatamente pois a velocidade tangencial reduz-se, ainda que a angular mantenha-se obviamente mesma, e como vê-se na equação abaixo, a aceleração centrípeta diminui conforme o raio diminui.
Assim, considerando esta parede e esta impossibilidade física mas argumento útil pelo que demonstraremos, consideraremos a densidade do ar a 1 atm, 1,225 kg/m³, e numa coluna de 2000 metros, teríamos uma massa de fáceis 2450 kg sobre minha cabeça - ou sola dos pés descalsos, para os mais exatistas que alongarem estes cálculos.
Para nosso caso, podemos aplicar a fórmula simples para a pressão de fluidos:
Para nosso caso, podemos aplicar a fórmula simples para a pressão de fluidos:
E teríamos uma pressão de 24010 kgm/s²/m², ou “Pascais”, e como cada Pascal é igual a 1/101325 atmosferas, temos que a pressão a que eu estaria submetido, pouco antes de ter todos os vasos rompidos, os intestinos explodindo e já a um bocado perdido meus olhos, seria de 0,2369 atmosferas, para o humano, algo não muito diferente do vácuo, com apenas mais alguns segundos de vida.
Poderíamos estender a análise dos fatos daquela atmosfera aberta para a perda de gases contínua que apresentaria, pois aqui mesmo na Terra continuamente perdemos gases, mesmo com nossa imensa atmosfera (digamos, comparada a rarefeita de Marte) e nossa significativa gravidade (que por outra via, é maior que a de Vênus, mas lá, com densidade muito maior, a pressão é imensamente maior que a nossa, 9,2 MPa), mas acredito que para efeitos didáticos, o erro em Física da concepção da estação já está bem apresentado.
Extras
I
Como profissional da química - ainda o sou, só o deixarei de ser provavelmente morto - as armas com características “químicas” me surpreenderam pela criatividade, fugindo dos espalhafatosos e pouco eficientes na prática “raios”.
www.heyuguys.co.uk
II
Um dos filmes que mostra bem os efeitos assustadores ao humano do vácuo, mesmo para curta exposição é O Enigma do Horizonte (IMDB), embora não esteja nesta lista:
Vacuum Exposure in Science Fiction - www.geoffreylandis.com
II
Um dos filmes que mostra bem os efeitos assustadores ao humano do vácuo, mesmo para curta exposição é O Enigma do Horizonte (IMDB), embora não esteja nesta lista:
Vacuum Exposure in Science Fiction - www.geoffreylandis.com
Abrindo esta página:
Como qualquer homem adequadamente treinado em boas condições de saúde, ele poderia sobreviver no vácuo por pelo menos um minuto - se ele tivesse tempo para se preparar para isso. Mas não houve tempo, ele só pode contar com os normais 15 segundo de consciência antes de seu cérebro estar faminto e a anoxia vencer. Mesmo assim, ele ainda pode se recuperar completamente após um ou dois minutos no vácuo - se ele foi corretamente recomprimido, demorou um longo tempo para que os fluidos do corpo para começar a ferver, em seus vários sistemas bem protegidos. - do “livro pós-filme” 2001, de Arthur C. Clarke
Uma divertida representação - para nossa atual tecnologia cinematográfica - está em Totall Recall - com o péssimo título no Brasil de “Vingador do Futuro” (1990, IMDB), mas para uma atmosfera como a de Marte, com sua pressão de 0,7 a 0,9 kPa (a da Terra é de 101,325 kPa).
Acerto em muitas coisas…
mas com erro sem o qual não haveria emoção
mas com erro sem o qual não haveria emoção
Assisti o filme Gravidade tanto em sala especial de certa rede de cinemas muito popular quanto numa sala IMAX.
O espetáculo é inegável. Mas tenho um problema com o apresentado, em especial, como a Síndrome de Kessler é apresentada.
Primeiramente, uma ilustração que nos será muito útil: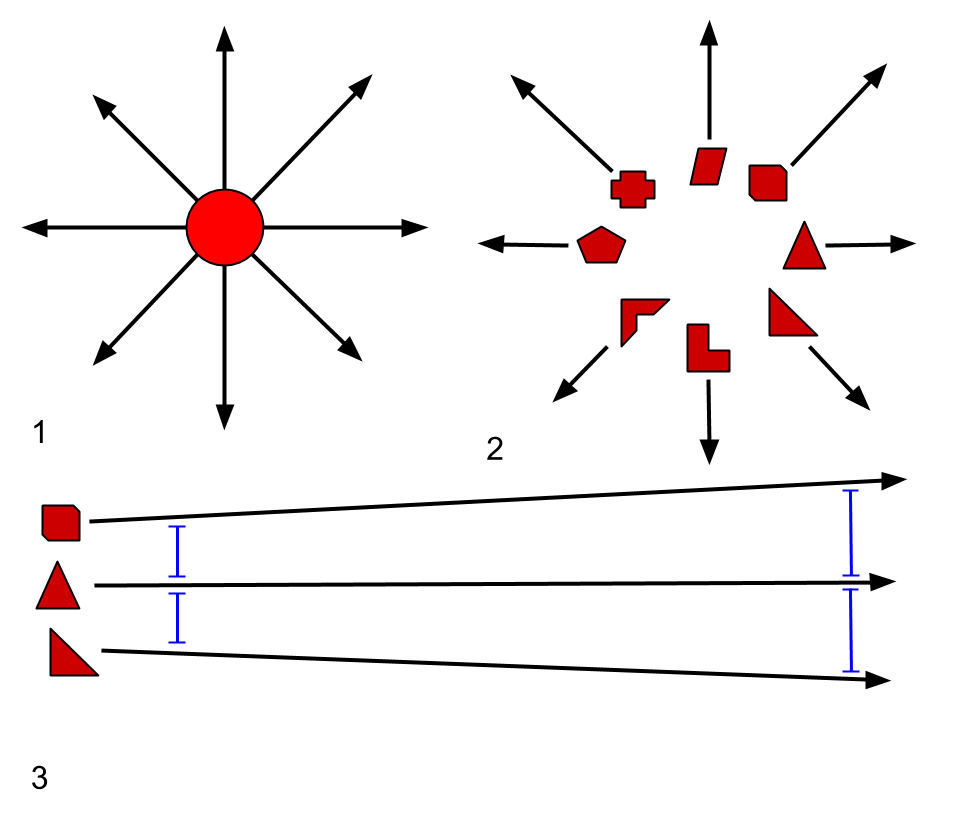
O espetáculo é inegável. Mas tenho um problema com o apresentado, em especial, como a Síndrome de Kessler é apresentada.
Primeiramente, uma ilustração que nos será muito útil:
Uma explosão é, a não ser por variações naturais ou desejadas, e com muito esforço, bastante homogeneamente excêntricas, ou, em termos mais simples, produz estilhaços em todas as direções, bastante bem distribuidos, o que em outras palavras ainda, sifginifica que não possui uma direção definida, portanto, possui “todas”.
Represento isto bem grosseiramente em [1], na ilustração acima, e ali, limito a representação a um plano.
Represento isto bem grosseiramente em [1], na ilustração acima, e ali, limito a representação a um plano.
Se esta explosão produz pedaços com várias direções, é de se perceber que esta direções produzirão somas ou subtrações da velocidade orbital dos corpos com que tai estilhaços colidirão da síndrome de Kessler. Pois bem, ao somar-se, tem-se de perguntar se esta soma não excedirá a velocidade orbital para aquela altura do corpo colidido, ou seja, este sairá da órbita “para cima”, escapando do - no caso - nosso planeta e sua atração gravitacional.
Pelo mesmo raciocínio, no caso da subtração (com redução de velocidade), o corpo “cairia”. A aula básica com o canhão no alto da montanha para se explicar as similaridades entre uma queda de um corpo, uma curva balística e uma órbita dão o entendimento do que aqui trato.
Pelo mesmo raciocínio, no caso da subtração (com redução de velocidade), o corpo “cairia”. A aula básica com o canhão no alto da montanha para se explicar as similaridades entre uma queda de um corpo, uma curva balística e uma órbita dão o entendimento do que aqui trato.
www.astro.virginia.edu
Por último, temos a “deflexão” o espalhamento dos projéteis/estilhaço, que comporta-se com densidade no inverso do quadrado da distância percorrida (lembremo-nos da terceira dimensão), ganhando mais e mais distância entre eles com o afastamento do local da explosão ou colisão, que corresponde num mundo tridimensional a um incremento da área, com redução do, assim digamos, fluxo de estilhaços (como espero que seja facilmente entendido em [3]).
A implicação disto tudo é que não haveria a densidade de estilhaços que mantem-se no magnificamente bem feito filme “acertando” sempre a Dra. Ryan Stone em suas desesperadas tentativas de sobreviver à catástrofe.
Por último, temos a “deflexão” o espalhamento dos projéteis/estilhaço, que comporta-se com densidade no inverso do quadrado da distância percorrida (lembremo-nos da terceira dimensão), ganhando mais e mais distância entre eles com o afastamento do local da explosão ou colisão, que corresponde num mundo tridimensional a um incremento da área, com redução do, assim digamos, fluxo de estilhaços (como espero que seja facilmente entendido em [3]).
A implicação disto tudo é que não haveria a densidade de estilhaços que mantem-se no magnificamente bem feito filme “acertando” sempre a Dra. Ryan Stone em suas desesperadas tentativas de sobreviver à catástrofe.
www.businessinsider.com
Mas notemos o “orbitar dos destroços”. Mesmo um intensa explosão - e foguetes nada mais são que explosões direcionais e relativamente, e muitas vezes nem tanto, controladas - não produziria a velocidade orbital, que chega a ser de dezena de km por segundo para os então ônibus espaciais, ou os satélites, telescópios espaciais e as estações espaciais. As colisões, menos ainda. Dois carros colidindo não somam sua velocidade “numa mesma direção”. Isso implicaria em passarem a formar um corpo com velocidade maior que as duas anteriores, o que contrariaria a conservação da energia. Soma-se a princípio apenas a sua quantidade de movimento, e mesmo assim, outros fatores teriam de ser analisados, como a própria dispersão em diversas direções desta energia/ quantidade de movimento, fora a transformação de parte da energia em calor, o que nos leva a questões das colisões em Física (guiadoestudante.abril.com.br).
Não perderei aqui mais tempo com estas nuances e detalhes, mas tratarei do que estou mantendo em foco: a velocidade orbital dos destroços não seria a mesma velocidade orbital tanto das estações espaciais quanto de nossa persistente em sobreviver astronauta, e o período orbital deles em relação a ela - triste alvo - não seria o mesmo que temos para ela e seus objetivos intermediários em sua descida para o conforto de nosso planeta. Haveria uma defasagem, um tempo que representaria quanto muito a diferença de “fase” entre sua órbita e a onda de destroços.
Mais Física de secundário aplicada…
Estes dias, uma moça caiu com o carro do vão central da ponte Rio-Niterói, de uma altura de 70 metros. (cbn.globoradio.globo.com)

www.baixaki.com.br
Para uma altura destas, com a massa de um carro, podemos esquecer desde o início a “velocidade terminal”, e veremos adiante que ela nem é realmente necessária como a ser colocada com o problema.
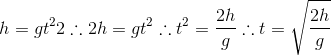
Para quem desejar editar Latex:
h={gt^2}{2}\therefore 2h=gt^2 \therefore t^2= \frac{2h}{g} \therefore t=\sqrt{\frac{2h}{g}}
Fazendo as contas: t≅3,78s (docs.google.com)
Como titio Aristóteles estava errado, e a infeliz Hipátia provavelmente demonstrou, e Galileu liquidou a questão de vez, não interessando a velocidade do carro sobre a ponte, a queda em sua velocidade na direção vertical se deu nestes 3,78 segundos, e obtem-se a velocidade de chagada na água pelo simples produto: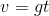
Para quem desejar editar Latex:
h={gt^2}{2}\therefore 2h=gt^2 \therefore t^2= \frac{2h}{g} \therefore t=\sqrt{\frac{2h}{g}}
Fazendo as contas: t≅3,78s (docs.google.com)
Como titio Aristóteles estava errado, e a infeliz Hipátia provavelmente demonstrou, e Galileu liquidou a questão de vez, não interessando a velocidade do carro sobre a ponte, a queda em sua velocidade na direção vertical se deu nestes 3,78 segundos, e obtem-se a velocidade de chagada na água pelo simples produto:
O que nos leva a pouco mais de 37 metros por segundo, ou uns 133,3 km/h.
Claro que a água, para um corpo como um carro, é um excelente “airbag”, mas a moça, com uma desacelação como a que deve ter sido causada, teve muita sorte.
Para explicar o acima digamos que o carro tenha entrado 5 metros na água, de onde caiu de 37m/s para zero de velocidade.
Lembrando:
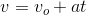 [1]
[1]
Mas:
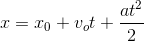 [2]
[2]
( x=x_0+v_ot+\frac{at^2}{2} )
Substituindo o que temos:
Para explicar o acima digamos que o carro tenha entrado 5 metros na água, de onde caiu de 37m/s para zero de velocidade.
Lembrando:
Mas:
( x=x_0+v_ot+\frac{at^2}{2} )
Substituindo o que temos:
De [1]:
E de [2]:
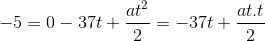 [4]
[4]
Aplicando [3] em [4]:
Ou seja: t≅0,09s e disto, tem-se que a desaceleração pela (equação [3]) foi da ordem de 411 m/s².
Tire-se a moça do carro no “voo” e o que mudaria seriam a dor e lesões.



