História da aritmética

Um dos trabalhos mais exigentes de toda minha colaboração para a Wikipédia, não pela complexidade do texto, mas pela língua da qual tive de traduzí-la, em sua primeira versão completa, ainda contendo muito por revisar, mas já num estado bem útil:

Tradução de ru.wikipedia.org - История арифметики

A história da aritmética abrange o período a partir do surgimento da contagem antes da definição formal dos números e operações aritméticas sobre eles por um sistema de axiomas. A aritmética - a ciência dos números, suas propriedades e relações - é uma das ciências matemáticas básicas, sendo está intimamente relacionada com álgebra e teoria dos números.

Aritmética, pintura de Pinturicchio, Aposento Borgia, 1492-1495. Roma, Palácio do Vaticano.

A aritmética tornou-se uma necessidade prática, a longo prazo, para medidas simples e cálculos. A primeira informação confiável sobre o conhecimento aritmética é encontrada nos monumentos históricos do antigo Egito e na Babilônia, relativa ao 3°-2° milênio a.C. Os matemáticos gregos tiveram grande contribuição para o desenvolvimento da aritmética, particularmente os pitagóricos, que tentaram usar números para identificar todas as leis do mundo. Na Idade Média, as principais áreas de aplicação da aritmética eram o comércio e os cálculos aproximados. A aritmética desenvolveu-se principalmente na Índia e países islâmicos, e só depois veio para a Europa Ocidental. Na astronomia náutica do século XVII, os cálculos de navegação, os cálculos de negócios mais complexos criaram novas solicitações aritméticas para a técnica de computação e deram um impulso promovendo seu desenvolvimento.

As bases teóricas do número como representação associadas principalmente com a definição de um número natural e axiomas de Peano foram formuladas em 1889. Foram seguidos pela definição estrita de números racionais, reais, negativos e complexos. A expansão adicional do conceito de número só foi possível nos casos de falhas de algumas das leis de aritmética.

O surgimento de aritmética

Se em dois conjuntos (conjunto de objetos), cada elemento do conjunto tem um único par no outro conjunto, consequentemente, estes conjuntos têm a mesma cardinalidade.[2] Tal comparação real, quando as coisas são dispostas em duas fileiras, foram usadas por tribos mais primitivas em trocas,[3] tornando-se possível estabelecer relações quantitativas entre grupos de objetos e não requerer o conceito de número.[4]

Entalhes em osso (Osso Ishango), mostrando contagem, encontrada perto do lago Edward, com mais de 30 mil anos [1]

Mais tarde, houve a contagem padrão natural, por exemplo, com os dedos e então o conjunto em padrões, tais como as mãos. Com o aparecimento de padrões que representam o número específico, e estes associados com um conceito de número. Além disso, foi comparado o número de indivíduos com a lua no céu, o número de olhos, o número de dedos em uma mão. Mais tarde, muitos padrões foram substituídos por um mais confortável, geralmente ele se tornaram dedos (5, 10) ou artelhos (mais 5, mais 10 na contagem, totalizando 20).[3]

O passo seguinte foi o surgimento de um conceito comum de número. Para o idioma europeu Proto-Indo, que usou o sistema de numeração decimal, nome de números já foram reconstruídos até cem, inclusive.[5] Lebesgue, nesta ocasião, disse: "É possível que, se as pessoas tivessem onze dedos, que seria aceita a notação unodecimal".[3]

Registrou-se os resultados de contagem usando entalhes em madeira ou osso, nós em cordas - marcações de contagem artificiais.[3][6][7] O osso rádio de um lobo jovem com 55 entalhes foi encontrado em 1937 perto da vila de Dolni Vestonice (República Checa). A idade do achado é de cerca de 5.000 anos (de acordo com outros dados, cerca de 30 mil anos [1]), sendo por um longo tempo, a mais antiga gravação conhecida.[6] B.A. Frolov, especialista em Paleolítico de Novosibirsk, vê nos padrões gráficos do Paleolítico Superior, começando com os monumentos de Dolni Vestonice, muitas evidências de que as pessoas desta era distinguiam claramente determinado números de elementos idênticos e certa quantidade, muitas vezes, enfatizou, sobre 5 ou 7 indivíduos, bem como múltiplos (especialmente 10 e 14).[8]

Ao nomear-se os números usou-se tanto nomes indecomponíveis (tais números são chamados de nós), ou nomes compostos por nomes algorítmicos..[9] Neste caso, uma combinação de algoritmos numéricos com base em operações aritméticas realizadas sobre os números nodais.[10]

A numeração, bem como os nomes de números, baseou-se em um dos três princípios:[6]

Aditivo (additio - adição) - indicações para 1, 10, 100, e repetição destes sinais (1n, 10n, 100n);

Subtrativo (subtractio - subtração) - uma combinação de números de mn, em que m n-m;

Multiplicativo (multiplicatio - multiplicação) - uma combinação de números equivalentes ao produto mn, usado para os nomes de dezenas e centenas nas línguas indo-europeias, em particular russos.

Para além do referido, um número de fontes como o princípio mencionado, com base na divisão.[11][12]

Textos matemáticos antigos e notações

Antigo Egito

Informações básicas sobre matemática egípcia baseada no Papiro Rhind, que é uma sinopse do escriba egípcio Ahmesa (século XVIII-XVII A.C.) e do papiro de Moscou. Ambos os papiro pertence à era do Império Médio. As informações sobre os textos matemáticos do Novo Reino, bem como os reinos primeiros e antigos, não sobreviveu.[13] Papiros matemáticos do Antigo Egito foram feitas para fins de ensino,[13] contendo problemas com soluções, informações de apoio e as regras de resolução números inteiros e frações, contento progressões aritméticas e geométricas, assim como suas equações.[7][14]  

Parte do papiro de Rhind.

Os egípcios usavam o sistema decimal.[15] Numeração hieroglífica era aditiva com caracteres especiais, e assim por diante até dez milhões, enquanto nos sinais hieráticos surgiram para os números de um a nove, para as dezenas, centenas e milhares, e caracteres especiais para frações de forma ou frações alíquotas.[16]  

Textos matemáticos egípcios focam o cálculo e as dificuldades que nele surgem, o que depende em grande medida dos métodos de resolução de problemas. Os egípcios usavam as operações aritméticas, como adição, duplicação e adição de frações a um. Qualquer multiplicação e divisão inteira sem qualquer resíduo foram realizados com operações repetitivas de duplicação, resultando em cálculos complicados, que foram assistidos por certos membros da seqüência 1, 2, 4, 8, 16,… [17] No Egito, foram usados ​​apenas fração em alíquotas, e todas as outras frações decompostas no valor de alíquotas. No Papiro Rhind apresentam-se tabelas de tais expansões por formas de frações, os cálculos com frações restantes vem com a operação de duplicação.[17] Ao determinar a área de uma superfície, o volume de um cubo ou encontrar o lado de uma área em função de sua área, os egípcios enfrentaram exponenciação e extração de raiz, embora os nomes destas operações ainda não era como os conhecemos.[17]

Babilônia

Textos matemáticos cuneiformes babilônicos usaram sistema numérico sexagesimal, característico dos sumérios,[19] e representados em um livro didático que inclui metodologias da multiplicação de números acima, bem como tabelas de números inversos, tábuas de quadrados e cubos de números naturais, cálculos de porcentagens e frações base.[7][15] Há mais de três centenas de tabuletas com textos, problemas matemáticos e tabelas numéricas.[20] A matemática babilônica é caracterizada pelo uso extensivo de tabelas.[21][22]

Tábua de argila babilônica com o cálculo = 1.41421296…

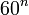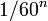Na Babilônia, apareceu pela primeira vez a numeração posicional consistente. Os primeiros cinquenta e nove números foram registrados com a repetição de personagens e dezenas de unidades necessárias várias vezes. Da mesma forma foram registrados múltiplos de sessenta à esquerda do primeiro conjunto. Mais tarde, este arranjo foi estendido para todo o número do formulário   e . Além disso, introduziu-se um sinal babilônio denotando zero quando da grafia do número.[22][23]

Adição e subtração na Babilônia eram as mesmas que aquelas ações em sistema posicional decimal com a diferença de que a transição para o próximo nível era necessária para o sistema de base, e para as unidades e dezenas. Devido à grande base dos babilônios não utilizava-se uma única tabela de multiplicação até 59, que contêm um grande número de elementos, e uma variedade de tabelas de números de 1 a 59 sobre os números 1, 2, 3, … 19, 20, 30, 40, 50 , também chamada de "capital". Na operação de divisão dos babilônios não era, portanto, dada muita atenção para as mesas de desenho de recíprocos, ou seja, números gerados quando dividido-se 60 2, 3, 40 .. No caso de divisão, dando fração infinita, primeiro escrevia-se que há um número inverso, e depois, dado um valor aproximado.[21]  

Ao resolver problemas aritméticos os babilônios invocavam proporção e progressão. Eles conheciam a fórmula para a soma dos termos de uma progressão aritmética, as regras para a soma de uma progressão geométrica, resolvendo o problema dos juros.[24] Na Babilônia, conhecia-se uma quantidade de trios pitagóricos, mas os métodos que usavam para encontrá-los é desconhecido. Em geral, o problema de encontrar soluções inteiros e racionais da equação 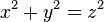refere-se à teoria dos números.[25] Problemas geométricos conduziram à necessidade de aproximar a raiz quadrada, utilizando a regra 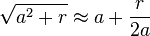e métodos iterativos para a prossecução da aproximação do resultado. [Nota 1][26]

Grécia antiga

Inicialmente, os gregos usaram a numeração ática, que usava símbolos para os números.[27] Este sistema é descrito em gramáticas pelo historiador de um rei Herodes no século II a.C.. Com numeração ática registra-se os resultados dos cálculos no ábaco. Ao longo do tempo, a numeração foi substituído pela alfabética compacta, ou iônica.[28] Numeração iônica usou as 24 letras do alfabeto grego e três letras extras de tratamento às unidades de 1 a 9, dezenas de 10 a 90 e centenas de 100 a 900 (lançadas a partir de cartas de circulação utilizadas para designar números 6, 90, 900[27]). Para distinguir o número de cartas sobre eles colocavam a linha. Para gravar o número 1000 utilizando o mesmo símbolo para a unidade, mas com um traço na parte inferior esquerda. Esta é uma reminiscência de um sistema posicional, mas a transição final ocorreu.[29]  Acredita-se que tal sistema dificultava cálculos complexos,[7] mas em 1882 o historiador da Matemática francês Paul Tannery chegou à conclusão de que a abordagem correta do sistema de numeração grego não é muito diferente dos cálculos decimais mais rápidos.[30]

Pitágoras, por Rafael Sanziol (parte da “Escola de Atenas”).

O desenvolvimento da aritmética grega deve-se principalmente à escola pitagórica. Pitagoreanos acreditavam em primeiro lugar, que a proporção de quaisquer dois segmentos podia ser expressa em termos da relação de números inteiros, consequentemente, geometria representava a aritmética de números racionais. Usar uma relação semelhante à harmonia da música levou os pitagóricos à conclusão de que todas as leis do mundo podiam ser expressas em termos de números e aritmética seria necessária a fim de formular um relacionamento e construir um modelo do mundo.[31]  Em particular, o pitagórico Arquitas de Tarento escreveu:[32] "Aritmética, na [minha] opinião, entre outras ciências muito distintas, perfeição do conhecimento; e a geometria [É perfeito porque] é mais clara do que a geometria, considerar qualquer [coisa]. "Aritmética, para a [minha] opinião, é entre outras ciências muito distinta em perfeição do conhecimento; e a geometria [é perfeito porque] é mais clara, pois a geometria considera qualquer [coisa].”

Os pitagóricos consideravam unicamente os números inteiros positivos, e acreditavam que o número de unidades de montagem.As unidades eram indivisíveis e dispostas em corpos geométricos regulares. Pitagóricos definiam a característica de "números agrupados" ("triangulares", "quadrados" e outros). Ao estudar as propriedades dos números, eles os dividiam em pares e ímpares (como um sinal de divisibilidade por dois), simples e compostos. Foram, provavelmente, os pitagóricos, utilizando apenas divisibilidade dois foram capazes de provar que, se  é um número primo, então 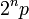é um número perfeito. A demonstração é dada nos "Elementos" de Euclides (IX, 36). Somente no século XVIII, Euler provou que outros números perfeitos existem, mas a questão de que se existem infinitos números perfeitos ainda não foi resolvida. Pitagóricos também desenvolveram uma fórmula e encontraram um número infinito de soluções inteiras da equação , os chamados trios pitagóricos [33] (a apresentação da primeira fórmula que determina os trios pitagóricos é atribuída a Platão, que dedicou muita atenção a aritmética, ou a ciência dos números [34]).

Sabe-se que entre os pitagóricos houve a doutrina dos números racionais, ou a relação dos segmentos, mas esta doutrina e suas demonstrações não sobreviveram.[35] No entanto, sobreviveram provas da incomensurabilidade da diagonal e o lado do quadrado unidade. Esta descoberta significa que a proporção de inteiros não é suficiente para expressar as relações de todos os segmentos e que, nesta base, é impossível construir uma geometria métrica [36] O primeiro pertence à doutrina das irracionalidades. Theaetetus, aluno de Sócrates, determinou que, para a superfície, cuja área é expressa por um número não-quadrado, o lado é incomensurável da superfície unidade. Em outras palavras, determinou o tipo de irracionalidade 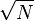. Da mesma forma, definiu a irracionalidade da diagonal para o cubo unidade (proporcional à raiz quadrada de 3).[37]

A teoria geral da divisibilidade apareceu em 399 a.C. e. pertence, evidentemente, também a Theaetetus. Euclides dedicou seu livro VII e parte do livro IX «Eu comecei". A teoria baseia-se no  algoritmo de Euclides para encontrar o máximo divisor comum de dois inteiros. A consequência deste algoritmo é a possibilidade de expandir qualquer número em fatores primos (“fatorar”), bem como a singularidade desta decomposição. A lei da singularidade de fatoração privilegiada é a base da aritmética dos números inteiros. O algoritmo de Euclides para determinar os quocientes parciais da expansão da fracão racional de um número racional. No entanto, o conceito de fração racional periódica não era possuído pelos gregos.[37]

Seguindo Euclides para números racionais, ao contrário, inteiros sempre tem possível divisão. Na Grécia, era-se capaz de operar com frações da forma 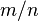, somar e subtraí-los, levando a um denominador comum, multiplicar e dividir, bem como subtrair. Em construções teóricas gregos partiam de uma unidade indivisível e não tratavam de frações de uma unidade, e a relação de números inteiros. Por estas relações definiram o conceito de proporcionalidade, que rompe todos as relações em classes disjuntas. Na antiga Grécia, determinava-se o menor par de todos tendo a mesma “atitude”, ou um ‘casal’, em que os números são relativamente primos, o que corresponde ao conceito de fração irredutível.[35]

O problema da construção de uma medida finita e a determinação de um número real foi uma crise científica no século V a.C.,  e a solução desses dilemas conduziu todas as escolas filosóficas da Grécia Antiga. Mostrar todas as dificuldades em resolver esses problemas conseguiu Zenão de Elea em seus paradoxos ou aporias.[38] Novos fundamentos da matemática foram sugeridos por Eudoxus de Cnidus. Formulou uma conceituação mais geral do que o número: o conceito de quantidades geométricas - por exemplo, a área do segmento, o volume. Para quantidades homogêneas Eudoxus determinou a função da relação entre os axiomas de ordem e introduziu o axioma, conhecido como o axioma de Arquimedes. Essa abordagem nos permitiu determinar os valores de relações arbitrárias, o que resolve o problema da incomensurabilidade então conhecido. No entanto, Eudoxus não formulou um análogo do axioma da continuidade, que é por isso que a questão da comensurabilidade não foi totalmente decidido. Eudoxus também não especificou valores para operações aritméticas.[39] Finalmente combinou o conceito do número e magnitude (ou mais precisamente, a relação com o valor da unidade padrão), como apresenta Isaac Newton, em "Aritmética Universal" (1707).[40] No entanto, a construção de Eudoxus é próximo à definição posterior de um número real dada por Dedekind para carta na qual Lipchitz requisita uma nova definição.[39]

Após as conquistas de Alexandre, o Grande, o centro da ciência grega mudou-se para Alexandria.[41] A dificuldade fundamental do tempo são os "Elementos" de Euclides, obra composta de treze livros. Livro V é dedicado à teoria das relações de Eudoxus, o livro VI - as relações de comunicação com os segmentos de operação de multiplicação ou a construção de paralelogramos, os livros VII-IX - a teoria de números inteiros e racionais, também considerado como linhas, o livro X - a classificação irracional sobre Theaetetus.[42]

No trabalho de Arquimedes o método do “O Contador de Areia” foi desenvolvido para a expressão de um grande número arbitrariamente. Seu projeto permite que se construa uma série de primeira ordem (até 108), em seguida, a segunda ordem (de 108 até 108.108) e, ainda, ao mesmo tempo pode ser expandido. Arquimedes também mostra que o número de grãos em uma esfera, cujo diâmetro é inferior a 10000 vezes maior que o diâmetro da Terra não excede 1063.[43][44]

Folha de "Aritmética", de Diofanto (o manuscrito é do século XIV). A linha superior contém a equação: .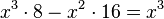

Com o passar do tempo, rumo à Idade Média, a aritmética da Grécia antiga, a matemática como um todo, declinou.[45] Novos conhecimentos só aparecem no século I-II a.C..[46] No século III começou a construção da álgebra de Diofanto não confiando na geometria e aritmética. Diofanto também expandiu a área do número com os números negativos.[47] Diofanto trabalhou na resolução de equações indeterminadas em números racionais, no cruzamento da teoria dos números e geometria algébrica.[48]

Roma antiga

O sistema de numeração romano não era bem adequado para a computação. Caracteres numéricos romanos apareceram posteriormente ao alfabeto e não são descendentes de suas anotações de cunho exclusivamente matemático. Acredita-se que os números originais de 1 a 9 são, respectivamente, o número de linhas na vertical, e a seu traço cruzado significava o número vezes dez (daí o número X). Consequentemente, para obter o número 100 anula-se a barra duas vezes. Subsequentemente, houve a simplificação do sistema.[49] Atualmente, ele é usado em casos especiais - século XIX, Caterina II, VI Congresso e outros.

China

No século II a.C. foram criados "Tratado sobre o pólo de medição" (astronomia) e “A matemática em nove livros" (um livro para agrimensores, engenheiros, funcionários públicos e comerciantes) - as mais antigas obras de matemática existentes da China. Juntamente com uma série de mais livros escritos nos séculos III-IV, eles formaram os "Dez tratados clássicos" que foram reimpressos por longo período inalterados.[50] Para os matemática do século XIV a China foi um conjunto de algoritmos numéricos para resolver um quadro de contagem.[51]

Triângulo Yang Hui (análogo ao Triângulo de Pascal), manuscrito chinês medieval, 1303.

No centro da numeração chinês está um princípio multiplicativo: são escritos a partir de cima para baixo ou da esquerda para a direita, enquanto que o sinal de milhares de milhares distancia-se mais para o número de centenas - um sinal de centenas, com o número de dezenas - um sinal de uma dúzia - e no final o número de unidades. Para executar operações aritméticas usa-se calculador suanpan e varas de contagem. Na placa de contagem usa-se registro posicional. Ao mesmo tempo, de acordo com o matemático chinês do século III Sun Tzu, "nos métodos que são usados ​​na análise convencional, especialmente [deve] se reunir com valores: unidades de dezenas verticais, horizontais; são centenas, milhares e dezenas têm a mesma aparência, dezenas de milhares e centenas, também ".[52]

As operações aritméticas de adição e subtração, produzidas na placa de contagem, não exigiram tabelas adicionais para tabela de multiplicação dos mesmos, como 1 x 1 a 9 x 9. Ações de multiplicação e divisão produzidas a partir dos valores mais significativos, e os resultados intermediários são removidas do tabuleiro, o que torna impossível a verificação. A princípio, as operações de multiplicação e divisão são independentes, mas, a esse tempo, Sun Tzu fez sua revisão.[53]  Quase simultaneamente com os números inteiros e as frações apareceu, já no século II a.C. operações com frações bem desenvolvidos. Para a adição e subtração de produto utilizando os denominadores, a multiplicação é geometricamente definida como a área de um retângulo, a divisão também foi associado com o problema da divisão de uma área, com o número de participantes na divisão podendo ser fracionado. No século V a.C. Zhang Qiu Jian substituiu a divisão por multiplicação por uma fração invertida, enquanto que a fração foi vista como um par de números, ajudado pelo uso da placa de contagem. Já no século III a.C. na China havia decimais, aos qual foi dado um valor aproximado de valores irracionais.[54]  

Na China, foram capazes de resolver problemas usando as regras de duas posições erradas, que os europeus atribuíram à ciência indiana. Por substituição por dois valores diferentes no lado esquerdo da equação 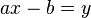para o lado direito a receber dois valores diferentes, dos quais utilizando-se proporções poderia se encontrar uma solução para 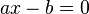. Os chineses usaram uma opção quando do lado direito há excesso ou deficiência.[55] Para a resolução de sistemas de equações lineares foi necessária a introdução de números negativos. Eles aplicaram na placa varas de uma cor diferente, e outra tinta sobre a carta ou barra. Além disso, os números negativos têm um nome especial. Para eles, as regras foram formuladas para operações de adição e subtração, com subtração determinada, em primeiro lugar. Inicialmente, os números negativos foram utilizados apenas na conta e no final dos cálculos foram removidas do tabuleiro, em seguida, os estudiosos chineses começaram a interpretá-los como uma dívida ou escassez.[56]

Aritmética na Idade Média

Na Idade Média, a matemática se desenvolve principalmente em países islâmicos, Bizâncio e da Índia, e só depois vem para a Europa Ocidental. Uma das principais áreas de matemática neste momento são a aritmética, cálculos e ensinamentos de aproximações comerciais sobre o número.[57]

Índia

O sistema de numeração posicional (dez dígitos, incluindo o zero) foi introduzido na Índia. Com ele foi permitido o desenvolvimento de regras relativamente simples de operações aritméticas.[7] Os pesquisadores acreditam que na Índia o sistema de posicionamento foi introduzido pela primeira vez o mais tardar no início de nossa era. No entanto, devido ao fato de os indianos utilizarem materiais frágeis para a escrita, poucos documentos resultantes deste período sobreviveram. Um documento autêntico, utilizando a numeração posicional, é considerado o manuscrito Bakhshaliyskaya (ou Bakhshali), que pertence ao século XII.[58]  

Para expressar números inteiros na Índia já utilizava-se o sistema decimal. Primeiro foram as figuras na carta Karosti (Kharosthi), em que foram escritos da direita para a esquerda, e depois na escrita Brāhmī, em que foram escritos da esquerda para a direita. Ambas as versões usam o princípio de adição para números até 100 e multiplicador para valores maiores. No entanto, em Brāhmī utiliza-se caracteres especiais para os números de 1 a 9. Na base deste sistema foram concebidos modernos números letras Devanagari (ou "letras divinas"), que foram utilizadas no sistema decimal posicional. Até o ano de 595 utilizava-se um primeiro número de entrada, que usava nove dígitos, não sendo incluído o zero. Por conveniência em cálculos, Aryabhata utilizou registros de números com sinais usando-se de letras em sânscrito. Em 662, o bispo cristão sírio North Sebohtpisal afirmou: "Eu não vou tocar em ciência os indianos... seu sistema numérico que ultrapassa qualquer descrição. Eu só quero dizer que o projeto é realizado por meio de nove personagens".[59]   

Estátua de Aryabhata no Centro de Astronomia e Astrofísica, em Pune.

Operações aritméticas básicas na Índia foram consideradas, como a adição, a subtração, a multiplicação, a divisão, em quadratura e do cubo, as raízes quadradas e cúbicas, que foram desenvolvidos pelas regras. Os cálculos foram realizados em placa contando com grãos de areia ou pó, ou simplesmente no chão escrevendo-se com varas. Cálculos intermediários foram apagados, resultando na incapacidade de se verificar usando a operação inversa, que era usada em vez de utilizar a prova dos noves.[60] Os indianos conheciam frações e foram capazes de realizar operações sobre elas, a proporção de progressão.[61] Já a partir do século VII a.C. eles usaram números negativos, interpretando-as como uma dívida, assim como números irracionais.[62] Eles foram atraídos pela soma de séries numéricae, em particular, exemplos de progressões aritméticas e geométricas estão disponíveis no "Vedas", e no século XVI Narayana Pandit fez um somatório mais geral.[63]

Os matemáticos indianos Aryabhata, Brahmagupta e Bhaskara resolveram equações diofantinas do tipo 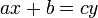em números inteiros. Além disso, eles resolveram em inteiros equações da forma 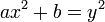que foi a maior conquista de matemáticos indianos na teoria dos números. Posteriormente, esta equação e seu caso especial quando 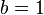atraiu a atenção de Fermat, Euler e Lagrange. Proposta pelo método de Lagrange para encontrar soluções foi perto pelos indianos.[64]

Países islâmicos

Nos séculos IX-X, o centro científico islâmico era Bagdá, onde trabalharam al-Khwarizmi, al-Hasib Habbash, al-Fargani, Thabit Ibn Qurra, Ibrahim ibn Sinan al-Battani. Mais tarde, houve novos centros de pesquisa em Bukhara, Khorezm e Cairo, onde trabalhou Ibn Sina, al-Biruni e Abu Kamil al-Misri, e, em seguida, em Isfahan e Maragheh, onde trabalharam Omar Khayyam e Nasir al-Din al-Tusi. No século XV o novo centro de pesquisa foi criada em Samarkand, em que trabalhou Ghiyas al-Din al-Kashi. Centros de matemática na costa noroeste da África e da Península Ibérica desempenharam um papel importante na disseminação do conhecimento na Europa.[65]

Os árabes usaram dois tipos de numeração: posicional alfabética e decimal. A numeração alfabética embora semelhante ao grego antigo, mas retornou ao alfabeto semita.[66] No início do século IX, Muhammad ibn Musa al-Khwarizmi escreveu um livro "Sobre o contar dos indianos". O livro contém resolução de problemas práticos "de vários tipos e variedades" e foi o primeiro livro escrito usando a notação posicional, antes que os dados utilizados para os cálculos estivessem apenas nem tábuas de contagem.[66][67] No século XII Adelardo (Espanha) e John Sevelskim (Inglaterra), realizaram duas traduções de livros para o latim.[68] Seu original não foi preservado, mas em 1857 sob o nome de "Alhorezmi incluindo o índio", foi publicado em uma tradução latina.[67] Em seu tratado descreve como realizar com a ajuda de numerais indianos na placa de contagem operações aritméticas, como adição, subtração, duplicação, multiplicação, divisão e raiz quadrada.[69] Multiplicação de frações como a divisão, considerando o uso de proporções: multiplicar esse era o mesmo que procurar 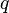, que 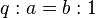. Esta teoria baseia-se na aritmética árabe. No entanto, houve outro cálculo de frações que representem qualquer fração como a soma das fracções alíquotas.[70]

Tradução em latim de página do livro "Por conta indiana".

Entre os anos 952-953, Abu al-Hasan Ahmad Abu'l-Hasan al-Uqlidisi em seu trabalho "O livro está dividido sobre aritméticas indianas" usando decimais, dividiu os números ímpares e realizou alguns outros cálculos, mas este livro não tem qualquer impacto sobre o desenvolvimento. No início do século XV al-Kashi tinha a intenção de construir um sistema de frações em que todas as operações seriam realizadas como com números inteiros e estariam disponíveis para aqueles que não sabem, "O cálculo de astrônomos".[70] Em 1427, al-Kashi descreveu o sistema decimal, que se espalhou na Europa após Simon Stevin em 1585.[7] Assim, al-Kashi formulou as regras básicas das operações com frações decimais, as fórmulas para  traduzi-los em sexagesimal e vice-versa.[70]

 

Nos trabalhos de al-Khwarizmi há a técnica comum de extrair a raiz quadrada, a extração de raízes cúbicas com Kushyar Gilani, o desenvolvimento total de métodos para o cálculo das raízes envolvida por Omar Khayyam. A primeira descrição da extração de raízes de qualquer grau de um inteiro é encontrado no livro de al-Tusi "Coleção de aritmética usando placas e pó" (1265). O sistema é essencialmente o mesmo que o esquema de Horner proposto no século XIX, quando a parte situa-se aproximadamente na forma de 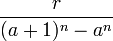. Além disso, al-Tusi forneceu uma tabela de coeficientes binomiais de uma forma semelhante ao triângulo de Pascal.[71] Muita atenção foi dada nos países árabes aos números irracionais e cálculos aproximados. Al-Khwarizmi produziu por operações simples com os radicais, que é mais simples do que os segmentos díspares utilizados na Grécia antiga. Desenvolve-se a teoria das proporções submetida à análise crítica. Em particular, Omar Khayyam em 1077, em seu tratado "Comentário para as dificuldades na introdução do livro de Euclides", apresenta que a definição grega antiga não reflete a verdadeira essência das proporções. Khayyam deu uma nova definição de proporção, introduziu a relação "mais" e "menos" para generalizar a noção de um número real positivo. Os números negativos não foram populares com os matemáticos árabes.[72]

Para resolver os problemas árabes apreciavam a regra tripla, vinda da Índia e descrita, juntamente com várias outras técnicas em "O Livro do Indiano Rashika", de al-Biruni, a regra das duas disposições falsas veio da China e recebeu justificativa teórica no "Livro do estado da falsa posição dupla" de Costa ben Luca.[73]

O sucesso da ciência islâmica na teoria dos números foi menos significativa. Eles foram capazes de resolver as equações do primeiro e segundo grau em números inteiros, conheciam as regras de construção de trios pitagóricos, e pela primeira vez foi feita uma declaração que a equação 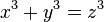geralmente era insolúvel em números racionais, o que é um caso especial do chamado último teorema de Fermat. A prova prevista desta afirmação não foi preservada,[74] sendo considerada em nossos dias como atribuída a Euler.

Bizâncio

O primeiro matemático cristão bizantino era Anfimov, que viveu no século VI. A aritmética bizantina foi influenciada pelas obras de matemáticos árabes e gregos. A Psell Michael, que viveu no século XI, pertence um ensaio sobre a aritmética, onde toca os números e as relações de classificação, bem como os principais nomes, graus, chamando ao mesmo tempo 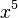“primeiro inefável", e 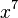- a "segunda inexprimível", que diz que Psell conhecia e usava o sistema multiplicativo em que os expoentes são expressos em produto e não acrescentando, como era anteriormente. A Maxim Planudu, que viveu no século XIII, pertencem comentários para o "Aritmética" de Diofante, e "Aritmética ao longo das linhas dos índios". No século XIV John Pedias escreveu vários tratados sobre aritmética, destacando suas perguntas difíceis, Nikolai Ravda levou ao método de cálculo dos dedos das mãos e um método aproximado para extrair raízes quadradas, e Isaac Argir, comentou sobre os primeiros seis livros dos "Elementos" de Euclides e construiu uma extração de tabela de raízes quadradas para os números até 102 utilizando as frações sexagesimais.[75]

América

Na América Central, usou-se principalmente o sistema numérico vigesimal. Sacerdotes maias na península de Yukatan usavam-no em cálculos abstratos (relacionados a simbolismo religioso, com enormes números de “ciclos” de seus mitos de criação) e em cálculos do calendário maia. Entre as limitações de seus métodos e resultados, certos cálculos, ainda que sofisticados em técnica e exatos resultados, só atingem o número 19 como um de seus fatores,[76] e com o uso de uma razão adicional para utilizar o número 5.[77] O calendário maia era um sistema posicional, onde cada item foi localizado relacionado com uma divindade e com um determinado número de caracteres. Ao escrever uma divindade não a está representando, e para designar um lugar vazio foi usado como um símbolo de um escudo aberto[78] ou o olho.[79][80] Na América do Sul, para o registro de números foi usada numeração nodal, ou um conjunto de “quipos”.[81]

Yupana usado para cálculos aritméticos.

Cálculos aritméticos foram realizadas utilizando yupany, que é um análogo do abaco,[82] no entanto, devido ao sistema de aritmética com números específicos, não relacionado com cálculos astronômicos, teve fraco desenvolvimento.[83]

Europa Ocidental

No feudalismo inicial na Europa Ocidental não necessitava da ciência não ir além das questões de aritmética prática e geometria. Os livros de “artes liberais” continham uma introdução para as sete artes liberais, incluindo aritmética. Foram as obras mais populares de Boécio, que datam do século VI, que, entre outras coisas, traduziram para o latim a "Aritmética" de Nicómaco de Gerasa com seus próprios exemplos numéricos e uma parte dos "Elementos" de Euclides sem prova rigorosa.[84]

Através da Espanha e Sicília no século X começou-se a amarrar os laços científicos com o mundo árabe. Neste momento, os cientistas visitaram o monge Gerbert, da Catalúnia, que mais tarde se tornou o papa Silvestre II. A ele são creditadas obras como o "Livro da divisão de números" e "Regras da conta no ábaco." Em ambos os livros os números são representados por palavras escritas ou algarismos romanos.[84] Herbert chamou cálculos sobre o ábaco de "abatsistami".[85]

Página do "Livro dos ábacos", de Fibonacci.

Nos séculos XII-XIII na Europa, haviam traduções latinas de livros árabes em aritmética. Traduções básicas foram feitas do árabe para a Península Ibérica, em Toledo, sob o patrocínio do arcebispo Raymond I, bem como em Barcelona e Segovia. As representações nos livros de numeração decimais posicional foram chamadas de "algoristami" em homenagem ao matemático al-Khwarizmi na forma Latina.[85] Aos poucos, o novo sistema prevaleceu.[68][86] Sua principal vantagem é a simplificação das operações aritméticas. No entanto, na Alemanha, França e Inglaterra, os novos números não seriam adotados antes do final do século XV.[86]

Esse conhecimento chegou até Leonardo Fibonacci, italiano de Pisa, que viveu no século XIII. Em sua principal obra "Liber Abaci" (Livro dos Ábacos), escrito em 1202, ele se tornou um defensor do sistema de numeração indiano e métodos de cálculo no ábaco considerando-os um desvio de uma caminho mais correto. Cinco capítulos do livro são dedicados à aritmética dos números inteiros. Fibonacci usou zero como um número real, realizou “provas dos nove”, sabia dos métodos para determinação da divisibilidade por 2, 3, 5, 9, trouxe a um denominador comum da fração usando o menor múltiplo comum dos denominadores, expôs a regra de três, as regras de cinco, sete, nove, e outras variáveis. Em regras de proporções, resolveu problemas que envolvem a mistura, operado pela soma da série, incluindo uma das séries de retorno e da série de Fibonacci, explicou o método de cálculo aproximado de raízes quadradas e cúbicas. No "Livro dos ábacos" são dadas em conjunto com a evidência de uma variedade de métodos e objetivos, que são amplamente utilizados nos escritos de matemáticos posteriores.[87]

O professor na Universidade de Oxford,  Mestre Thomas Bradwardine (início do século XIV), que se tornou mais tarde arcebispo de Canterbury, o livro pertence a "aritmética teórica", que é uma versão abreviada de "aritmética" de Boécio. Além disso, o pensador em seu trabalho sobre os mecanismos do uso da "metade", com base no qual o matemático francês Nicole Oresme desenvolveu a doutrina do expoente fracionário em seu tratado "Relações de algorismos", e foi para o conceito de expoentes irracionais,[88][89] que pode ser celebrado entre inteiro o suficiente perto e fracionário, e realizou uma generalização de exponenciação com expoentes fracionários positivos. Seus trabalhos foram publicados apenas no século XIX.[89]

Em 1484 o manuscrito foi publicado pela “bachelor” francesa de medicina Nikola Shyuke em "Ciência dos números em três partes", em que ele, em particular, compara o trabalho dos membros de uma progressão aritmética e a soma de uma progressão geométrica, em antecipação a logaritmos, considera casos de raiz do primeiro grau de si mesma e usa expoentes negativo e zero.[90] Em 1487 Pacioli escreveu o seu "A quantidade [de conhecimento] em aritmética, geometria, relações e da proporcionalidade". Nesse livro, publicado em Veneza em 1494, Pacioli delineou vários métodos de operações aritméticas, aproveitando os símbolos algébricos. Além disso  Pacioli indicou o sinal 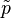, adição, e subtração - 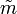. Também usou em números negativos a expressão "inferior a zero" e formulou a regra que muda o sinal quando multiplica-se números.[91]

A página título da edição flamenga de "Dezena".

O texto de Cardano, "Grande Arte", no século XVI, introduziu o conceito de valores imaginários, ou sofísticos. Embora Cardano considerou-os inúteis, eles foram usados ​​por Rafael Bombelli para resolver equações cúbicas, que também introduziu a regra da multiplicação do imaginário e os números reais.[92] No mesmo século na Europa estavam se espalhando o conceito e uso de decimais. Eles aparecem na obra de François Vieta, Immanuel Bonfisa, Simon Stevin. Em 1585, em seu livro "A Décima", última campanha para o uso generalizado de casas decimais. No mesmo ano em "Aritmética",[93] ele deu uma nova definição de número irracional como "por meio do qual é expresso o número de todas as coisas”. Stevin considerado números irracionais e em parte negativas, tais como estes, bem como frações e pensou em unidades divisíveis.[94]

Stiefel em sua "Aritmética Completa" apresenta uma definição de algoritmo e a razão entre a relação de divisão,[95] também dá uma interpretação geométrica dos números negativos ("menos do que nada") e faz uma analogia entre a introdução dos números negativos e irracionais.[96] Em 1569, o professor francês Peter Ramus, que foi proibido pelo decreto do rei de criticar Aristóteles escreveu: "O curso de matemática em o livro de trinta e um", que tentou dar a matemática um novo estudo, baseado não na geometria e aritmética.[97]

Aritmética da Idade Moderna

Na astronomia náutica do século XVII, a mecânica, nos cálculos de negócios mais complexos criaram novas solicitações aritméticas para a técnica de computação e deram um impulso para promover o desenvolvimento.

Aritmética decimal e a extensão do conceito

O conceito de número sofreu uma mudança significativa. Anteriormente o campo dos números atribuía apenas apenas números racionais positivos, e desde o século XVI, cada vez mais reconhece-se os números irracionais e negativas. As "atualizações" de Descartes em 1637 estabelecem uma ligação entre a aritmética e as construções geométricas, utilizando proporções, em outras palavras, o número é entendido no mesmo sentido que o de Euclides e as operações aritméticas são equivalentes à busca da relação desejada de comprimento para a relação já apresentada. A razão de qualquer comprimento para a unidade, neste caso, é equivalente a um número real, e os argumentos serão verdadeiras tanto para comparáveis ​​e para os segmentos díspares. O próprio Descartes trata esses últimos de "números de surdos» (nombres sourds). Newton em suas palestras divide-os em três tipos: inteiros (medidos em unidades), fracionários (múltiplos de uma unidade) e irracionais (incomensuráveis com a unidade). Desde 1710 essa definição é firmemente inserida em todos os livros texto.[98]

A fração periódica apareceu no "Cálculo Decimal"  (Logistica decimalis) de I.G. Beyer em 1603. os trabalhos sobre eles continuaram por Valais em "Tratado sobre Álgebra" (Treatise on Algebra), em 1685, onde se determinou que uma fração irredutível 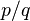, o número de dígitos será menor do que ou igual a .  Wallis também mostra a imagem final com um denominador da forma 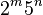,  também sabendo que é impossível expressar os números irracionais em frações periódicas.[99]

No início do século XVII Napier inventou os logaritmos. O uso de logaritmos e o ponto decimal, a inclusão do conceito de aritmética dos números irracionais como uma sequência de aproximações racionais ampliou o âmbito da aritmética até o final do século XVII e identificou a importância fundamental dessa ciência para o estudo das variáveis contínuas.[7]

Tabelas aritméticas, 1835.

No século XVIII continuou-se a trabalhar com decimais, em particular com os decimais infinitos e periódicos. O fato de qualquer fração periódica ser um número racional, e que qualquer fração irredutível contendo o denominador diferente dos dois e cinco fatores primos pode ser expandida numa periódica, foi demonstrado na metade meio do século XVIII por Lambert. No trabalho de “Pesquisa aritmética” de Gauss utilizando a teoria de “resíduos de energia”, foram  apresentadas propriedades mais profundas de frações periódicas. No entanto, os livros didáticos da época que passam decimais afetadas não o mencionam. Frações contínuas foram estudadas por Euler, que primeiro introduziu as técnicas de transformação de infinitas frações contínuas em séries infinitas, e, em seguida, dedicou um capítulo inteiro no primeiro volume de sua "Introdução à Análise do Infinito", em 1748. A Euler pertence a prova de que cada número racional pode ser representado como uma fração contínua finita, e que uma fração periódica continua com unidades no numerador representa a raiz da equação quadrática. O reverso foi comprovado por Lagrange em 1768.[99] No século XVIII com Euler e seus discípulos a aritmética toma formas modernas.[7]

Albert Girard e Descartes interpretaram os números negativos geometricamente na direção oposta do segmento. Apesar do fato de Descartes apresentar raízes negativos de equações, juntamente com as raízes reais positivas (em oposição a imaginária), algumas propriedades de números negativos por longo tempo permaneceram obscuras.[100] Em 1° de setembro de 1742, Euler em uma carta a Nicholas Bernoulli primeiro avançou a alegação de que as raízes de todas as equações algébricas são 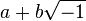. Em 1747, em "Reflexões sobre a causa comum de ventos" D'Alembert mostrou que 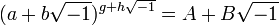. O "Estudo sobre as raízes imaginárias" de Euler, no entanto, um número imaginário é definido como aquele que "não superior a zero ou inferior a zero ou igual a zero", e "algo impossível." Ele prova o teorema que cada soma imaginária forma um número real 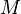e o produto de um número real de 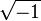. O problema foi resolvido pelas funções individuais, a gama de operações em números imaginários não foi delineada. Além disso, houve problemas com a interpretação geométrica de números imaginários.[101] A primeira tentativa foi feita por Wallis, que acreditava que o número imaginário de segmentos, perpendicular ao real [100] e foi o trabalho de Heinrich Kühn em 1753, em que considerava um lado número imaginário da área com uma área de negativo.[101] Wallis conseguiu desenvolver, isoladamente, mas simultaneamente com Caspar Wessel e Jean-Robert Argand na virada do séculos XVIII-XIX. [100]

Criação e desenvolvimento da teoria dos números

Na década de 30 do século XVII a teoria dos números era colocada por Fermat como uma área não separada da aritmética, e sua opinião era de que apenas seria um pouco afetada por Euclides e, possivelmente, por Diofanto. Trabalhos de Fermat eram engajados na solução de equações diofantinas e da divisibilidade de números inteiros. Ele fez uma série de afirmações sem provas, nomeadamente das pequenas e último teorema de Fermat.[102][103] Fermat não tem nenhum trabalho especial sobre a teoria dos números, e apresentam-se apenas em notas em correspondência, bem como comentários à "Arimética” de Diofanto.[104]

Só depois de 70 anos Fermat atraiu a atenção de Euler, que estudou a teoria dos números por várias décadas.[104] A ela é dedicada quatro volumes e meio da série de 30 volumes de Euler sobre Matemática.[105] Euler estudou a generalização do pequeno teorema de Fermat, e a prova do último teorema de Fermat para o caso 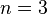. Euler foi o primeiro a ter aplicado a problemas da teoria dos números outros ramos da matemática, especialmente a análise pelo Teorema de Euler na Teoria dos Números (Teorema do Tociente). Formulou um método de funções geradoras, a identidade de Euler, bem como problemas associados com a adição de números primos.[106]

Acredita-se que, após o trabalho de teoria dos números de Euler, a teoria dos números tornou-se uma ciência separada.[107]

Estudo dos problemas aritméticos

A partir das obras de geometria de Lobachevsky desencadeou-se um processo associado de revisão crítica dos fundamentos da matemática, que aconteceu no século XIX. Mesmo no século XVIII, foram feitas tentativas para dar uma justificativa teórica do número de vários pontos de vista. No começo isso era apenas a aritmética dos números naturais, que são usados ​​para uma variedade de axiomas e definições que são muitas vezes excessivas e insuficientes, enquanto em grande parte emprestadadas dos "Elementos" de Euclides. É também o caso com as leis básicas da aritmética: leis comutativa e associativa para adição e multiplicação mencionados muitas vezes, a lei distributiva para a multiplicação em relação à adição - menos e todas as cinco leis - são extremamente raras. Leibniz primeiro definiu a tarefa de construção dedutiva da aritmética e, em particular, havia mostrado a necessidade de provar a igualdade "dois mais dois é igual a quatro" em seu "Novo Ensaio sobre o Entendimento Humano" em 1705. Na tentativa de resolver este problema e seus axiomas foi apresentada por Wolf em 1770, Schultz em 1790, Ohm em 1822, Grassmann em 1861 e, finalmente, Peano em 1889.[108]

Giuseppe Peano.

A complexidade das afirmações das principais divisões da aritmética contrasta com a simplicidade de suas posições iniciais. Apenas no meio do século XIX Grassmann escolheu  um sistema de axiomas básicos que definem adição e multiplicação. O sistema permite que você visualize as disposições restantes da aritmética como uma consequência lógica dos axiomas. Com base nos axiomas foram provadas as propriedades comutativa, associativa e as leis distributivas de adição e multiplicação, o conceito de frações como pares de números inteiros com certas leis e comparações. O trabalho de Grassmann continuou o de Peano.[7] Houve outras tentativas para se aproximar de uma fundamentação teórica completa da aritmética dos números naturais, em especial o trabalho de Hilbert, enquanto não surgia em 1932 a demonstração dos teoremas de incompletude de Gödel.[108]

Da mesma forma, tem havido tentativas de dar uma justificativa teórica das frações racionais, para a qual haviam dois conceitos: A parte igual da unidade ou a razão de dois valores homogêneos.[108] Para funções racionais necessários para provar a lealdade para com as igualdades e 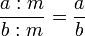( 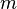— número natural), que foram usadas em adição, subtração e redução de frações. As igualdade era trivial na teoria das relações, mas não são claras, independentemente da sua concepção. No entanto, elas apenas eram “sentidas como verdade”.[109] A aritmética das frações foi justificada por J. Tannery em 1894, em sua fração modelo apresentando pares de números inteiros.[101]

Em 1758, na "Primeira fundação da aritmética, geometria, trigonometria esférica e plana e perspectivas", Kestner pediu o apoio de todos os conceitos de aritmética através de um número inteiro. Assim, determina-se no livro números inteiros, frações, números negativos, decimais, números irracionais, e só então a teoria das relações. Operações em números irracionais começaram a ser exploradas explorar, com base na sua aproximação por frações racionais. Ao mesmo tempo, a existência de números irracionais foi feita antecipadamente, e eles foram tratados como fora da sequência de números racionais. Para uma definição de números irracionais utilizados por Newton como a razão de valores incomensuráveis ​​(tal definição foi dada por Euler). Da mesma forma tratados os números irracionais por P. Rakhmanov na "Nova teoria da detenção e proporções geométricas quantidades proporcionais e incomensuráveis, e, neste último caso com base na teoria de limites." E apenas na segunda metade do século XIX, existe uma teoria rigorosa dos números reais formulado Meresya, Cantor, Dedekind e Weierstrass.[109]

Na teoria da formação dos números negativos, o principal problema foi a afirmação de que o número negativo é menor que zero, então não é menos do que nada. Na definição estrita de números negativos faltava, embora tenham havido tentativas de formular regras de sinais ("menos vezes mais dá um sinal de menos" e "menos vezes menos dá mais"). O matemático francês Carnot escreveu em 1813: "A Metafísica de regras assinala um estudo mais profundo mostrando que é talvez mais difícil do que a metafísica de quantidades infinitesimais; Normalmente, isso nunca foi provado de forma totalmente satisfatória e, aparentemente, ela não pode mesmo ser demonstrada de forma satisfatória. " As primeiras tentativas para formular uma teoria de números negativos foi feitas no meio do século XIX e pertencem a Hamilton e Grassmann.[110]  

A interpretação geométrica dos números complexos foi proposta por Caspar Wessel na "Experiência da representação analítica de tendências e suas aplicações, principalmente para a solução plana e polígonos esféricos" em 1799. Wessel quis trabalhar com a direção do segmento no plano, com a ajuda de operações algébricas, mas os números reais só permitem mudar na direção oposta, mas não especificar uma direção arbitrária. Wessel utilizou unidades básicas 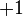, , 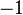, 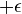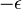e. usando a regra da multiplicação, concluiu que . O trabalho de Wessel passou despercebido por cerca de 100 anos. Durante esse tempo, sua interpretação dos números imaginários, foi apresentada por Jean Robert Argand nos anos 1813-1814, Shayss em 1831 na "Teoria de resíduos biquadrados" e Hamilton em 1832, que construiu a teoria aritmética, considerando os números complexos como pares de reais.[101]

Wessel tentou estender a teoria do espaço tridimensional, mas não teve êxito. A questão permanece em aberto enquanto Hamilton não construiu uma teoria de quatérnions, que quando multiplicado pela lei comutativa essa não é cumprida. Neste estudo Weierstrass, Frobenius e Pierce revelaram que renunciar a qualquer das leis da aritmética tem alguma expansão para além do conceito de números complexos.[101]  

História da aritmética na Rússia

Na Rússia, usa-se a analogia da numeração grega usando cirílico ou glagolítico. No entanto, ao contrário de muitos povos que atribuíram valores numéricos em novas textos, na Rússia com algumas exceções continuou-se a usar letras gregas, ou similares. Os números foram escritos na mesma maneira que acentuados, que está entre o 15 primeiro sinal orientado para e em seguida, cinco a dez, enquanto entre os 25 - 2 em primeiro lugar, em seguida, para 5, a mais difundida sendo a numeração acirílica.[111] A aritmética na Rússia foi chamada щётная мудрость (sabedoria “schёtnaya”), ou "Livro Negro", onde havia magia negra. Poucos podiam ler e entender livros sobre aritmética, pois eles continham regras e cálculos aritméticos que foram compostos por personagens obscuras.[30]

"Aritmética", de Magnitsky.

Datam do século XI os problemas matemáticos de uma coleção "Verdade Russa" (Русская Правда, Russkaya Pravda),  - os primeiros documentos matemáticos existentes da antiga Rússia, contendo problemas sobre resíduos (lixo), pecuária e a quantidade de grãos e feno, colhidos a partir de determinadas áreas. Um maior desenvolvimento da ciência foi interrompido com a invasão mongol-tártara.[112] No final do século XVI haviam os livros “Recom na aritmética grega”, “Algorismos Alemães”, e em russo, “Sabedoria Tsifirnaya Contando”, que, de acordo com Karamzin, foi a primeira aritmética russa.[113]

Acredita-se que os algarismos arábicos foram introduzidas na Rússia após a primeira viagem ao exterior de Pedro I,[114] quando em 1698 ele trouxe de Londres oficiais da Marinha. Um dos policiais foi Fergarson, que se acredita ter introduzido algarismos arábicos na Rússia.[113] Mas, na verdade, eles chegaram a Rússia muito antes de Pedro, em 1647, em Moscou, sob o czar Alexei Mikhailovich foram impressos em regulamentos militares russos, que costumavam conter algarismos arábicos. Livros são impressos em russo fora da Rússia contendo algarismos arábicos, desde o início do século XVI. No texto usando numeração eslava, e para os cálculos, algarismos árabes.[115]  

Em 1682, em Moscou, foi publicado o primeiro livro de conteúdo matemático "Lendo fácil, todo homem Kupuyuschy ou vendendo extremamente delícias confortáveis, o número de todos os tipos de coisas”, que continha as tabelas de multiplicação até 100 e usava ​​a numeração eslava. A segunda edição deste livro foi lançada em 1714 em São Petersburgo, foi impresso e continha algarismos arábicos. Em 1699, em Amisterdan publicou-se um livro "Resoluções rápidas e úteis em aritmética, ou no ensino e aprendizagem de qualquer conta em qualquer combinação de coisas” - o primeiro livro de aritmética em russo. O livro foi compilado por Ilya Fedorovich Kopievichem (ou Kopievsky) comerciante comissionado de Arkhangelsk. Ele não satisfez o cliente, e não recebeu comissões pela distribuição.[115]

Na Rússia, o primeiro livro de aritmética, de Leonti Magnitsky, foi publicado em 1703.[114] A "Aritmética" de Magnitsky, depois no resto da Europa, usou a contagem para o número de dedos: os números de 1 a 9 são chamados de "dedos" - o zero, "nem", as dezenas - "comboios", e outros números - "escritos".[Nota 2][116]

Notas

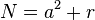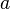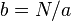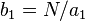1. Suponha que você precise encontrar a raiz de   ,  — uma primeira aproximação em desvantagem,  — em aproximação por abundância. A segunda abordagem é formada pela fórmula da média aritmética , e corresponde a , etc.[26]

2. Em Herbert (940-1003) usou-se «digiti», «articuli», «compositi». Em Leonardo Pyzanskoho (início do século XIII) - «unitates», «deceni», «décadas». Nos autores da época do Renascimento - «monadici», «décadas».[116]  

Referências

1. 1 2 Boyer & Merzbach, 2010, Concepts and Relationships
2. MacDuffee, C. C. Aritmética (Eng.). Encyclopædia Britannica. Retirado em 20 de março de 2012. Arquivado da fonte original em 28 de maio de 2012.
3. 1 2 3 4 История математики (História da Matemática), т. I, 1970, pp. 9—12.
4. Депман, 1965, с. 18—20.
5. Mallory, J. P. Encyclopedia of Indo-European Culture / J. P. Mallory, Q. A. Douglas. — L. : Fitzroy Dearborn Publishers, 1997. — P. 398. — ISBN 9781884964985.
6. 1 2 3 История математики, т. I, 1970, с. 12—13.
7. 1 2 3 4 5 6 7 8 9 Арнольд, 1970.
8. Фролов, Б. А. Числа в графике палеолита. (Números paleolíticos na carta) — Новосибирск : Наука, 1974. — С. 93—94.
9. Арифметика, 1951, с. 12—13.
10. Арифметика, 1951, с. 24.
11. Беллюстин, 1909, Глава 4: Различные системы счисления (Capítulo 4: Diferentes sistemas numéricos).
12. Меннингер, 2011, с. 100.
13. 1 2 История математики, т. I, 1970, с. 19—20.
14. Scott, 1958, p. 8.
15. 1 2 Депман, 1965, p. 49—52.
16. История математики, т. I, 1970, с. 21.
17. 1 2 История математики, т. I, 1970, с. 23—24.
18. История математики, т. I, 1970, с. 25.
19. История математики, т. I, 1970, с. 34.
20. История математики, т. I, 1970, с. 35.
21. 1 2 История математики, т. I, 1970, с. 37—39.
22. 1 2 Scott, 1958, p. 10.
23. История математики, т. I, 1970, с. 36.
24. История математики, т. I, 1970, с. 40.
25. История математики, т. I, 1970, с. 50.
26. 1 2 История математики, т. I, 1970, с. 46—47.
27. 1 2 Scott, 1958, pp. 40—41.
28. История математики, т. I, 1970, с. 62.
29. История математики, т. I, 1970, с. 64.
30. 1 2 Депман, 1965, с. 53—54.
31. История математики, т. I, 1970, с. 67.
32. История математики, т. I, 1970, с. 68.
33. История математики, т. I, 1970, с. 68—69.
34. Scott, 1958, p. 20.
35. 1 2 История математики, т. I, 1970, с. 70—72.
36. История математики, т. I, 1970, с. 73.
37. 1 2 История математики, т. I, 1970, с. 74—76.
38. История математики, т. I, 1970, с. 88—89.
39. 1 2 История математики, т. I, 1970, с. 94—98.
40. История математики, т. II, 1970, с. 33—35.
41. История математики, т. I, 1970, с. 106.
42. История математики, т. I, 1970, с. 111—114.
43. История математики, т. I, 1970, с. 128.
44. Выгодский, 1967, с. 265.
45. История математики, т. I, 1970, с. 139.
46. История математики, т. I, 1970, с. 143.
47. История математики, т. I, 1970, с. 144—146.
48. История математики, т. I, 1970, с. 146—148.
49. Депман, 1965, с. 57—58.
50. История математики, т. I, 1970, с. 156—157.
51. История математики, т. I, 1970, с. 178.
52. История математики, т. I, 1970, с. 157—160.
53. История математики, т. I, 1970, с. 160—161.
54. История математики, т. I, 1970, с. 162—163.
55. История математики, т. I, 1970, с. 163—164.
56. История математики, т. I, 1970, с. 167—169.
57. История математики, т. I, 1970, с. 154.
58. Депман, 1965, с. 62—68.
59. История математики, т. I, 1970, с. 181—183.
60. История математики, т. I, 1970, с. 183—185.
61. История математики, т. I, 1970, с. 185.
62. История математики, т. I, 1970, с. 190—191.
63. История математики, т. I, 1970, с. 201.
64. История математики, т. I, 1970, с. 194—195.
65. История математики, т. I, 1970, с. 205—209.
66. 1 2 История математики, т. I, 1970, с. 209—210.
67. 1 2 Депман, 1965, с. 72—78.
68. 1 2 Депман, 1965, p. 90—94.
69. История математики, т. I, 1970, с. 211—212.
70. 1 2 3 История математики, т. I, 1970, с. 212—214.
71. История математики, т. I, 1970, с. 214—216.
72. История математики, т. I, 1970, с. 216—218.
73. История математики, т. I, 1970, с. 218—219.
74. История математики, т. I, 1970, с. 227—229.
75. История математики, т. I, 1970, с. 249—250.
76. Меннингер, 2011, с. 80—81.
77. Меннингер, 2011, с. 83—84.
78. Ifrah, 2000, p. 310.
79. Boyer & Merzbach, 2010, Early Number Bases.
80. Депман, 1965, с. 61.
81. Депман, 1965, с. 59.
82. Ifrah, 2000, p. 308.
83. Ifrah, 2000, p. 322.
84. 1 2 История математики, т. I, 1970, p. 254—256.
85. 1 2 История математики, т. I, 1970, с. 256—257.
86. 1 2 Арифметика, 1951, с. 50—57.
87. История математики, т. I, 1970, с. 261—265.
88. История математики, т. I, 1970, с. 270—271.
89. 1 2 История математики, т. I, 1970, с. 275—277.
90. История математики, т. I, 1970, с. 289—290.
91. История математики, т. I, 1970, с. 286—287.
92. История математики, т. I, 1970, с. 296—297.
93. История математики, т. I, 1970, с. 301—303.
94. История математики, т. I, 1970, с. 304—306.
95. История математики, т. I, 1970, с. 306—307.
96. История математики, т. I, 1970, с. 316.
97. История математики, т. I, 1970, с. 307.
98. История математики, т. II, 1970, с. 34—36.
99. 1 2 История математики, т. III, 1972, с. 45—47.
100. 1 2 3 История математики, т. II, 1970, с. 36—39.
101. 1 2 3 4 5 История математики, т. III, 1972, с. 61—66.
102. История математики, т. II, 1970, с. 74.
103. История математики, т. II, 1970, с. 78.
104. 1 2 История математики, т. II, 1970, с. 73—74.
105. История математики, т. III, 1972, с. 37—38.
106. Чисел теория / А. А. Карацуба // Чаган — Экс-ле-Бен. — М. : Советская энциклопедия, 1978. ( Enciclopédia Soviética ) — (Большая советская энциклопедия : в 30 т. / гл. ред.А. М. Прохоров ; 1969—1978, т. 29) ( Grande Enciclopédia Soviética )
107. История математики, т. II, 1970, с. 17.
108. 1 2 3 История математики, т. III, 1972, с. 47—49.
109. 1 2 История математики, т. III, 1972, с. 49—52.
110. История математики, т. III, 1972, с. 52—56.
111. История математики, т. I, 1970, с. 252.
112. История математики, т. I, 1970, с. 252—253.
113. 1 2 Арифметика, наука ( Aritmética, ciência ) // Энциклопедический словарь Брокгауза и Ефрона (Dicionário Enciclopédico Brockhaus e Efron ) : В 86 томах (Nos volumes ) (82 т. и 4 доп. ( Adicional ) ). — СПб., 1890—1907.
114. 1 2 Успенский, Г. П. Опыт повествования о древностях русских. (  Experimente a história de antiguidades da Rússia ) — Харьков : Университетская типография, 1818. — С. 532. — 818 с.
115. 1 2 Депман, 1965, p. 90—94.
116. 1 2 Депман, 1965, p. 90—94.

Literatura

• Беллюстин, В. Как постепенно дошли люди до настоящей арифметики. ( Como as pessoas gradualmente chegaram a esta aritmética ) — М. : Типография К. Л. Меньшова, 1909.
• Выгодский, М. Я. Арифметика и алгебра в древнем мире.( Aritmética e álgebra no mundo antigo ) — М. : Наука, 1967. — 370 с.
• Депман, И. Я. История арифметики. (História da aritmética ) — М. : Просвещение, 1965. — 400 с.
• Меннингер, К. История цифр. Числа, символы, слова. (Números, símbolos, palavras) — М. : ЗАО Центрполиграф, 2011. — 543 с. — ISBN 9785952449787.
• Boyer, C. B. A History of Mathematics : [англ.] / C. B. Boyer, U. C. Merzbach. — John Wiley & Sons, 2010. — 640 p.
• Ifrah, G. The Universal History of Numbers : [англ.]. — John Wiley & Sons, 2000. — 635 p. — ISBN 0471393401.
• Scott, J. F. A History of Mathematics From Antiquity to the Beginning of the Nineteen Century : [англ.]. — L. : Tailor & Francis Ltd, 1958. — 266 p.
• Арифметика / В. И. Арнольд ( Vladimir Arnold ) // Ангола — Барзас. — М. : Советская энциклопедия ( Angola - Barzas. - Enciclopédia Soviética ), 1970. — (Большая советская энциклопедия ( Grande Enciclopédia Soviética ) : в 30 т. / гл. ред.А. М. Прохоров ; 1969—1978, т. 2).
• История математики ( História da Matemática ) : в 3 т. / под ред. А. П. Юшкевича ( Adolf Yushkevich ) . — М. : Наука, 1970. — Т. I : С древнейших времён до начала Нового времени ( ИНТЕРНЕТ БИБЛИОТЕКА - BIBLIOTECA ONLINE - История математики - História da Matemática - Desde os tempos antigos até início do período moderno ).
• История математики  ( História da Matemática ) : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1970. — Т. II : Математика XVII столетия ( Matemática do século XVII ).
• История математики : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1972. — Т. III : Математика XVIII столетия ( Matemática do século XVIII ).
• Энциклопедия элементарной математики / под ред ( Enciclopédia de matemática elementar /  ). П. С. Александрова ( Pavel Alexandrov ), А. И. Маркушевича и А. Я. Хинчина. — М. : Государственное издательство технико-теоретической литературы ; Л., 1951. — Кн. 1 : Арифметика. ( Aritmética ) — 448 с.