sexta-feira, 10 de julho de 2015

Matemática da relatividade geral - I





A matemática da relatividade geral (RG) refere-se a várias estruturas matemáticas e técnicas que são utilizadas no estudo e formulação da teoria da relatividade geral (RG) de Albert Einstein. As principais ferramentas utilizadas nesta teoria geométrica da gravitação são campos tensores definidos sobre uma variedade Lorentziana representando espaço-tempo. Este artigo é uma descrição geral da matemática da RG.

O motivo da escolha de tensores

O princípio da covariância geral afirma que as leis da física devem ter a mesma forma matemática em todos os referenciais e tal foi um dos princípios centrais no desenvolvimento da relatividade geral. O termo 'covariância geral' foi utilizado na formulação inicial da RG, mas agora é referido por muitos como covariância de difeomorfismo. Embora covariância de difeomorfismo não seja a característica definidora da relatividade geral [Nota 1], e permanecem controvérsias quanto ao seu estado presente na RG, a propriedade de invariância de leis físicas implicadas no princípio aliado ao fato de que a teoria é essencialmente de caráter geométrico (fazendo uso de geometrias que não são euclidianas) sugeriu que a RG fosse formulada usando a linguagem de tensores. Isto será discutido mais adiante.
Espaço-tempo como uma variedade
A maioria das abordagens modernas para a matemática da RG começam com o conceito de uma variedade. Mais precisamente, a construção física básica que representa a  gravitação - um espaço-tempo curvo - é modelada por uma variedade Lorentziana de quatro dimensões, derivável (“suave”) e conectada. Outros descritores físicos são representados por várias tensores, discutidas abaixo.
A justificativa para a escolha de uma variedade como a estrutura matemática fundamental é refletir propriedades físicas desejáveis. Por exemplo, na teoria das variedades, cada ponto está contido em uma (não significando exclusiva) carta de coordenadas, e este gráfico pode ser considerado como representando o 'espaço-tempo local' em torno do observador (representado pelo ponto). O princípio da covariância de Lorentz local, que afirma que as leis da relatividade especial mantém-se localmente sobre cada ponto do espaço-tempo, presta um apoio adicional para a escolha de uma estrutura de variedade para representar o espaço-tempo, como localmente em torno de um ponto em uma variedade geral, a região “parece", ou se aproxima muito de um espaço de Minkowski (espaço-tempo plano).
A idéia de coordenar gráficos como "observadores locais que podem realizar medições na sua vizinhança” também faz sentido físico, dado que este é realmente como um coletor de dados físicos - localmente. Para problemas cosmológicos, um gráfico de coordenadas pode ser muito grande.

Estrutura local versus mundial
Uma distinção importante na física é a diferença entre as estruturas locais e globais. Medidas em física são realizadas em uma região relativamente pequena do espaço-tempo e esta é uma razão para estudar a estrutura local do espaço-tempo na RG, ao passo que a determinação da estrutura do espaço-tempo global é importante, especialmente em problemas cosmológicos.

Um problema importante na RG geral é dizer quando dois espaços-tempos são "o mesmo", pelo menos localmente. Este problema tem suas raízes na teoria de variedades onde determinar se duas variedades de Riemann da mesma dimensão são localmente isométricas ('localmente a mesmo "). Este último problema foi resolvido e sua adaptação para a RG é chamado o algoritmo de Cartan-Karlhede.

Tensores na relatividade geral
Uma das consequências profundas da teoria da relatividade foi a abolição de quadros de referência privilegiados. A descrição de fenômenos físicos não deve depender de quem faz a medição - um quadro de referência deve ser tão bom quanto qualquer outro. A relatividade especial demonstrou que nenhum referencial inercial era preferencial a qualquer outro referencial inercial, mas preferiu referenciais inerciais sobre quadros de referência não inerciais. A RG eliminou preferência por referenciais inerciais, mostrando que não há quadro de referência preferencial (só por inércia ou não) para descrever a natureza.
Qualquer observador pode fazer medições e as grandezas numéricas precisas obtidas dependem apenas do sistema de coordenadas usado. Isto sugeriu uma maneira de formular a relatividade usando "estruturas invariantes ', aquelas que são independentes do sistema de coordenadas (representadas pelo observador) usado, mas ainda tendo uma existência independente. A estrutura matemática mais adequado parecia ser um tensor. Por exemplo, quando se mede os campos elétricos e magnéticos produzidos por uma carga em aceleração, os valores dos campos dependerão do sistema de coordenadas utilizado, mas os campos são considerados como tendo uma existência independente, esta independência representada pelo tensor eletromagnético.
Matematicamente, tensores são operadores lineares generalizados - mapas multilineares. Como tal, as idéias de álgebra linear são empregadas para estudar tensores.
Em cada ponto \scriptstyle \, p de uma variedade, o espaço tangente e cotangente à variedade nesse ponto podem ser construídas. Vetores (por vezes referidos como vetores contravariantes) são definidos como elementos do espaço tangente e covetores (às vezes denominados vetores covariantes, mas mais comumente vetores duais ou “um-formas”) são elementos do espaço cotangente.
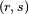Em \scriptstyle \, p, estes dois espaços vetoriais podem ser utilizados para construir tensores do tipo \scriptstyle \, (r,\, s), que são mapas multilineares de valor real que atuam sobre a soma direta de \scriptstyle \, r cópias do espaço co-tangente com \scriptstyle \, s cópias do espaço tangente. 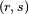O conjunto de todos estes mapas multilineares forma um espaço vetorial, chamado espaço produto tensor do tipo \scriptstyle \, (r,\, s) em \scriptstyle \, p e denotado por 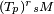\scriptstyle \, (T_p)^r{}_sM. 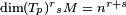Se o espaço tangente é n-dimensional, pode ser mostrado que \scriptstyle \dim (T_p)^r{}_sM \;=\; n^{r+s}.

Na literatura de RG, é convencional utilizar o componente sintaxe para tensores.
Um tensor do tipo 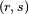\scriptstyle \, (r,\, s) pode ser escrito como:
T \;\! = \;\! {T^{a_1 \ldots a_r}}_{{b_1} \ldots {b_s}} \frac {\partial} {\partial x^{a_1}} \otimes \ldots \otimes \frac {\partial} {\partial x^{a_r}} \otimes dx^{b_1} \otimes \ldots \otimes dx^{b_s}


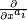Onde \scriptstyle \frac {\partial} {\partial x^{a_i}} é uma base para o espaço tangente i-ésimo e \scriptstyle dx^{b_j} uma base para o j-ésimo espaço cotangente
Como o espaço-tempo é assumido como sendo de quatro dimensões, cada índice de um tensor pode ser um de quatro valores. Assim, o número total de elementos que um tensor possui é igual a 4R, onde R é a soma dos números de índices covariantes e contravariantes no tensor (um número chamado de classificação (rank), ou “posto” do tensor).

Tensores simétrico e antissimétrico
Algumas grandezas físicas são representados por tensores, tendo não todas as quais os componentes independentes. Exemplos importantes destes tensores incluem tensores simétricos e antissimétricos. Tensores antissimétricos são comumente usados para representar rotações (por exemplo, o tensor vorticidade).
Embora um tensor de posto R genérico em 4 dimensões tenha 4R componentes, restrições sobre o tensor, como simetria ou antissimetria servem para reduzir o número de componentes distintos. Por exemplo, um 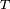posto dois simétrico satisfaz tensores e possui 10 componentes independentes, ao passo que um 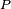posto dois antissimétrico (inclinação simétrica) satisfaz tensores e tem 6 componentes independentes. Para postos superiores a dois, os pares de índices simétricos ou antissimétricos devem ser explicitamente identificados.
Tensores antissimétricos de posto 2 desempenham papéis importantes na teoria da relatividade. O conjunto de todos esses tensores - muitas vezes chamado de bivetores - forma um espaço vetorial de dimensão seis, às vezes chamado espaço bivetor.
O tensor métrico
O tensor métrico é um objeto central na RG que descreve a geometria do espaço-tempo local (como um resultado da resolução das equações de campo de Einstein). Usando aproximação de campo gravitacional fraco, a métrica também pode ser considerada como representando o ‘potencial gravitacional’. O tensor métrico é muitas vezes chamado apenas de 'a métrica’.
A métrica é um tensor simétrico e é uma importante ferramenta matemática. Para além de ser utilizada para tensores de índices mais altos e baixos, também gera as conexões que são utilizadas para construir as equações geodésicas de movimento e o tensor de curvatura de Riemann.
Um meio conveniente de expressar o tensor métrico em combinação com os intervalos de distâncias incrementais de coordenadas a que se refere, é através do elemento de linha:
ds^2 = g_{ab} \, dx^a \, dx^b
Esta forma de expressar a métrica foi usada pelos pioneiros da geometria diferencial. Enquanto alguns relativistas consideram a notação ser um pouco antiquada, muitos alternam facilmente entre esta e a notação alternativa:
g = g_{ab} \, dx^a \otimes dx^b
O tensor métrico é comumente escrito como uma matriz 4 por 4. Esta matriz é simétrica e, assim, tem 10 componentes independentes.
Invariantes
Uma das características centrais da RG é a idéia de invariância de leis físicas. Este invariância pode ser descrita de muitas maneiras, por exemplo, em termos de covariânciad locais de Lorentz, o princípio geral da relatividade, ou covariância de difeomorfismo.
Uma descrição mais explícita pode ser dada usando tensores. A característica crucial dos tensores utilizados nesta abordagem é o fato de que (uma vez que uma métrica é dada) a operação de contrair um tensor de categoria R sobre todos os índices R dá um número - um invariante - que é independente da coordenada gráfica se usa para efetuar a contração. Fisicamente, isso significa que se o invariante é calculado por quaisquer dois observadores, eles vão receber o mesmo número, o que sugere que o invariante tem algum significado independente. Alguns invariantes importantes na relatividade incluem:

- o escalar de Ricci: \scriptstyle R \;=\; R^{ab}g_{ab}
- o escalar de Kretschmann: 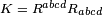\scriptstyle K \;=\; R^{abcd}R_{abcd}
Outros exemplos de invariantes em relatividade incluem os invariantes eletromagnéticos, e vários outros invariantes de curvatura, alguns desses encontrando aplicação no estudo de entropia gravitacional e a hipótese de curvatura de Weyl.


Classificação de tensores
A classificação dos tensores é um problema puramente matemático. Em RG, no entanto, certos tensores que têm uma interpretação física podem ser classificados com as diferentes formas do tensor geralmente correspondentes a algo físico. Exemplos de classificações de tensores úteis na RG geral incluem a classificação de Segre do tensor de energia-momento e a classificação Petrov do tensor de Weyl. Existem vários métodos de classificação desses tensores, alguns dos quais utilizam invariantes do tensor.
Campos tensoriais na relatividade geral
Campos tensoriais sobre uma variedade são mapas que atribuem um tensor para cada ponto da variedade. Esta noção pode ser tornada mais precisa através da introdução da idéia de um feixe de fibras, que, no presente contexto, significa coletar juntos todos os tensores em todos os pontos da variedade, assim, “agregando-os” todos em um grande objeto chamado feixe de tensores. Um campo tensorial é então definido como um mapa da variedade para o feixe tensorial, cada ponto p sendo associado com um tensor em p.
A noção de um campo tensorial é de grande importância na RG. Por exemplo, a geometria em torno de uma estrela é descrita por um tensor métrico em cada ponto, de modo que em cada ponto do espaço-tempo deve ser dado o valor da métrica para resolver os caminhos de partículas materiais. Outro exemplo são os valores dos campos elétricos e magnéticos (dado pelo tensor campo eletromagnético) e a métrica em cada ponto em torno de um buraco negro carregado para determinar o movimento de uma partícula carregada num tal campo.
Campos vetoriais são uma classificação de campos tensorais contravariantes de posto um. Campos de vetores importantes na relatividade incluem a quadrivelocidade, 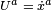\scriptstyle U^a \;=\; \dot{x}^a, a qual é a distância em coordenadas percorrida por unidade de tempo próprio, a quatriaceleração 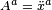\scriptstyle A^a \;=\; \ddot{x}^a e a quadricorrente 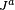\scriptstyle \, J^a descrevendo a carga e densidades de corrente. Outros campos tensores fisicamente importantes na relatividade incluem os seguintes:
  • O tensor de energia-momento \scriptstyle \, T^{ab}, um tensor simétrico de posto 2.
  • O tensor de campo eletromagnético \scriptstyle \, F^{ab}, um tensor assimétrico de posto 2.
Embora a palavra 'tensor' refira-se a um objeto em um ponto, é prática comum se referir a campos tensoriais em um espaço-tempo (ou uma região do mesmo) como apenas "tensores”.
Em cada ponto de um espaço-tempo em que uma métrica é definida, a métrica pode ser reduzida à forma de Minkowski usando a lei de inércia de Sylvester.
Derivadas de tensores
Antes do advento da RG, mudanças nos processos físicos eram geralmente descritas por derivadas parciais, por exemplo, ao descrever mudanças em campos eletromagnéticos (como nas equações de Maxwell). Mesmo na relatividade especial, a derivada parcial é ainda suficiente para descrever tais alterações. No entanto, em RG, verifica-se que as derivadas que são também tensores devem ser usadas. As derivadas têm algumas características comuns, incluindo de que eles são derivadas ao longo de curvas integrais de campos vetoriais.
O problema na definição de derivadas em variedades que não são planas é que não há maneira natural para comparar vetores em diferentes pontos. Uma estrutura extra em uma variedade geral é necessária para definir derivadas. Abaixo encontram-se descritos duas importantes derivadas que podem ser definidas mediante a imposição de uma estrutura adicional na variedade em cada caso.
Conexões afins
A curvatura de um espaço-tempo pode ser caracterizada por tomar-se um vetor em algum ponto e transportando-o em paralelo ao longo de uma curva no espaço-tempo. Uma conexão afim é uma regra que descreve como mover legitimamente um vetor ao longo de uma curva na variedade sem mudar sua direção.
Por definição, uma conexão afim é um mapa bilinear 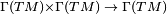\scriptstyle \Gamma(TM)\times\Gamma(TM) \;\rightarrow\; \Gamma(TM), onde 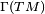\scriptstyle \,\Gamma(TM) é um espaço de todos os campos de vetores no espaço-tempo. O mapa bilinear pode ser descrito em termos de um conjunto de coeficientes de conexão (também conhecido como símbolos de Christoffel), especificando o que acontece com componentes de vetores de base no âmbito do transporte paralelo infinitesimal:
\nabla _{e_i} e_j = \Gamma ^k _{ji} e_k
Apesar da sua aparência, os coeficientes de conexão não são os componentes de um tensor. De um modo geral, existem D3 coeficientes de conexão independentes em cada ponto do espaço-tempo. A conexão é chamada simétrica ou livre de torção, se 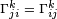\scriptstyle \Gamma^k_{ji} \;=\; \Gamma^k_{ij}. Uma conexão simétrica tem no máximo 1⁄2D2(D + 1) coeficientes únicos.
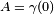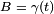Para qualquer curva \scriptstyle \gamma e dois pontos \scriptstyle A \;=\; \gamma(0) e \scriptstyle B \;=\; \gamma(t) sobre esta curva, uma conexão afim dá origem a um mapa de vetores no espaço tangente em A em vetores no espaço tangente em B:
X(t) \, = \Pi_{0,t,\gamma} X(0)
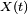e \scriptstyle \, X(t) pode ser computado em termos de componentes, resolvendo a equação diferencial
\frac{d}{dt} X^i(t) = \nabla_{C(t)} X^i(t) = \Gamma^i_{jk} X^j(t) C^k(t)
\scriptstyle \, C^j(t) sendo o vetor tangente à curva no ponto \scriptstyle \gamma(t).
Uma conexão afim importante na RG é a conexão de Levi-Civita, que é uma conexão simétrica obtida a partir de um vetor transportado paralelamente ao longo de uma curva tangente ao mesmo tempo mantendo o produto interno do vetor constante ao longo da curva. Os coeficientes de conexão resultantes (símbolos de Christoffel) podem ser calculados diretamente a partir da métrica. Por esta razão, este tipo de conexão é muitas vezes chamado de conexão métrica.
A derivada covariante
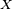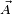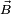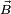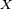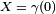Considere-se \scriptstyle X um ponto, \scriptstyle \vec A um vetor localizado em \scriptstyle X, e \scriptstyle \vec B um campo vetorial. A ideia de se diferenciar \scriptstyle \vec B em \scriptstyle X ao longo da direção \scriptstyle \vec A de uma maneira fisicamente significativa pode fazer sentido encolhendo-se uma conexão afim e uma curva suave parametrizada \scriptstyle \gamma\,(t) tal que \scriptstyle X \;=\; \gamma(0) e \scriptstyle \vec A \;=\; {d \over dt}\gamma(0).
A fórmula
\nabla _{\vec A} \vec B(X) = \lim_{\epsilon \rightarrow 0} \frac{1}{\epsilon}\left[\Pi_{(\epsilon,0,\gamma)} \vec B(\gamma[\epsilon]) - \vec B(X)\right]


para uma derivada covariante de 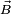\scriptstyle \vec B ao longo de 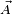\scriptstyle \vec A associado com a conexão 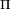\scriptstyle \,\Pi acaba por dar resultados independentes da curva e pode ser usado como uma "definição física" de uma derivada covariante.
Ela pode ser expressa utilizando coeficientes de conexão:
\nabla _{\vec Y} \vec X = X^a{}_{;b}Y^b \frac {\partial} {\partial x^a} = (X^a{}_{,b} + \Gamma ^a _{bc}X^c)Y^b \frac {\partial} {\partial x^a}
A expressão entre parêntesis, chamado um derivada covariante de 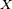\scriptstyle X (com respeito à conexão) e indicado por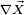\scriptstyle \nabla \vec X, é mais frequentemente utilizada nos cálculos:
\nabla \vec X = X^a{}_{;b} \frac {\partial} {\partial x^a} \otimes dx^b = (X^a{}_{,b} + \Gamma ^a _{bc}X^c) \frac {\partial} {\partial x^a} \otimes dx^b
Uma derivada covariante de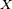\scriptstyle X pode então ser vista como um operador diferencial atuando sobre um campo vetorial remetendo-o a um tensor do tipo (1, 1) ('aumentando o índice covariante por 1') e pode ser generalizado para atuar em um campo tensorial tipo (r, s) remetendo aos campos tensoriais do tipo (r, s + 1). As noções de transporte paralelo pode então ser definidas da mesma forma como para o caso de campos vetoriais. Por definição, uma derivada covariante de um campo escalar é igual à derivada regular do campo.
Na literatura, existem três métodos comuns de denotar diferenciação covariante:
D_a T^{b \dots c}_{d\dots e} = \nabla_a T^{b \dots c}_{d \dots e} = T^{b\dots c}_{d\dots e;a}
Muitas propriedades padrão de derivadas parciais regulares também se aplicam às derivadas covariantes:


Em Latex:

\begin{align}
 \nabla_a (X^b + Y^b) &= \nabla_a X^b + \nabla_a Y^b \\
  \nabla_a (X^b Y^c)  &= Y^c (\nabla_a X^b) + X^b (\nabla_a Y^c) \\
  \nabla_a (f(x) X^b) &= f \nabla_a X^b + X^b \nabla_a f = f \nabla_a X^b + X^b {\partial f \over \partial x^a} \\
     \nabla_a (c X^b) &= c \nabla_a X^b, \quad c \text{ sendo constante}
\end{align}
Na RG, normalmente refere-se a essa como "a" derivada covariante, a qual é aquela associada com a conexão afim de Levi-Civita. Por definição, a conexão de Levi-Civita preserva a métrica sob transporte paralelo, portanto, a derivada covariante dá zero quando atua em um tensor métrico (assim como seu inverso). Isso significa que nós podemos tomar o  tensor métrico (inverso) dentro e fora da derivada e usá-la para aumentar e diminuir índices:
\nabla_a T^b = \nabla_a (T_c g^{bc}) = g^{bc} \nabla_a T_c
A derivada de Lie
Outra derivada tensorial importante é a derivada de Lie. Ao contrário da derivada covariante, a derivada de Lie é independente da métrica, embora em geral em RG utiliza-se uma expressão que aparentemente depende da métrica através da conexão afim. Enquanto a derivada covariante requer uma conexão afim para permitir a comparação entre os vetores em diferentes pontos, a derivada de Lie utiliza uma congruência a partir de um campo vetorial para atingir a mesma finalidade. A ideia de “arrasto” de Lie de uma função ao longo de uma congruência leva a uma definição da derivada de Lie, onde a função “arraste” é comparada com o valor da função original num dado ponto. A derivado de Lie pode ser definida para os campos tensoriais de tipo (r, s) e, a este respeito pode ser vista como um mapa que remete um tensor de tipo (r, s) para um tipo de (r, s).
A derivada de Lie é usualmente denotada por 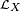\scriptstyle \mathcal L_X, onde 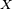\scriptstyle X é o campo vetorial ao longo do qual a congruência da derivada de Lie é tomada.
A derivada de Lie de qualquer tensor ao longo de um campo vetorial pode ser expressa por meio das derivadas covariantes desse campo tensorial e vetorial. A derivada de Lie de um escalar é apenas a derivada direcional:
\mathcal L_X \phi = X^a \nabla_a \phi = X^a \frac{\partial \phi}{ \partial x^a}


Objetos de classificação mais elevada recebem termos adicionais quando a derivada de Lie é tomada. Por exemplo, o derivado de Lie de um tensor do tipo (0, 2) é:
\mathcal L_X T_{ab} = X^c \nabla_c T_{ab} + (\nabla_a X^c)T_{cb} + (\nabla_b X^c) T_{ac} = X^c T_{ab,c} + X^c_{,a} T_{cb} + X^c_{,b} T_{ac}
Mais genericamente,
\begin{align} &\mathcal L_X T ^{a_1 \ldots a_r}{}_{b_1 \ldots b_s} = X^c(\nabla_cT^{a_1 \ldots a_r}{}_{b_1 \ldots b_s}) - \\ & \quad (\nabla_cX ^{a_1}) T ^{c \ldots a_r}{}_{b_1 \ldots b_s} - \ldots - (\nabla_cX^{a_r}) T ^{a_1 \ldots a_{r-1}c}{}_{b_1 \ldots b_s} + \\ & \quad (\nabla_{b_1}X^c) T ^{a_1 \ldots a_r}{}_{c \ldots b_s} + \ldots + (\nabla_{b_s}X^c) T ^{a_1 \ldots a_r}{}_{b_1 \ldots b_{s-1} c} \end{align}
De fato, na expressão anterior, pode-se substituir a derivada covariante 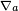\scriptstyle \nabla_a com qualquer conexão livre de torção \scriptstyle \tilde\nabla_a ou localmente, com a derivada dependente de coordenadas \scriptstyle \partial_a, mostrando que a derivada de Lie é independente da métrica. A derivada covariante é conveniente no entanto, porque ela comuta com o elevar abaixar dos índices.
Um dos principais usos da derivada de Lie na RG é no estudo de simetrias do espaço-tempo onde tensores ou outros objetos geométricos são preservados. Em particular, a simetria de Killing (simetria do tensor métrico sob arrastamento de Lie) ocorre muito frequentemente no estudo do espaço-tempo. Usando a fórmula acima, podemos escrever a condição que deve ser satisfeita por um campo vetorial para gerar uma simetria de Killing:
\begin{align} \mathcal L_X g_{ab} &= 0 \\ \Leftrightarrow \nabla_a X_b + \nabla_b X_a &= 0 \\ \Leftrightarrow X^c g_{ab,c} + X^c_{,a} g_{bc} + X^c_{,b} g_{ac} &= 0 \end{align}

Notas

1. A característica definidora (idéia física central) da relatividade geral é que a matéria e a energia causam que a geometria do espaço-tempo ao redor seja curvada.



Referências
  • Einstein, A. (1961). Relativity: The Special and General Theory. New York: Crown. ISBN 0-517-02961-8.
  • Misner, Charles; Thorne, Kip S. & Wheeler, John Archibald (1973). Gravitation. San Francisco: W. H. Freeman. ISBN 0-7167-0344-0.
  • Landau, L. D. and Lifshitz, E. M. (1975). Classical Theory of Fields (Fourth Revised English Edition). Oxford: Pergamon. ISBN 0-08-018176-7.

Postado por às

Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)