Finalmente, publico o conjunto de notas da série "Matemática indiana".
Inscrição budista em uma caverna em uma rota comercial através de Naneghat, oeste da Índia, de cerca de 100 a.C., que descreve o número 17 em algarismos “não-posição-valor” para 10 e 7. - S.G. DANI; Understanding ancient Indian mathematics - www.thehindu.com
Notas
1. Encyclopaedia Britannica (Kim Plofker) 2007, p. 1
2. (Hayashi 2005, pp. 360–361)
3. Ifrah 2000, p. 346: "The measure of the genius of Indian civilisation, to which we owe our modern (number) system, is all the greater in that it was the only one in all history to have achieved this triumph. Some cultures succeeded, earlier than the South Asian cultures, in discovering one or at best two of the characteristics of this intellectual feat. But none of them managed to bring together into a complete and coherent system the necessary and sufficient conditions for a number-system with the same potential as our own." - Tradução: “A medida do gênio da civilização indiana, à qual devemos o nosso sistema (numérico) moderno, é tanto maior na medida em que era o único em toda a história a ter conseguido esse triunfo. Algumas culturas conseguiram, mais cedo do que as culturas do sul da Ásia, a descoberta de um ou no máximo duas das características desta façanha intelectual. Mas nenhum deles conseguiu reunir, em um sistema completo e coerente, as condições necessárias e suficientes para um sistema de números com o mesmo potencial como o nosso.”
4. Plofker 2009, pp. 44–47
5. Bourbaki 1998, p. 46: "...our decimal system, which (by the agency of the Arabs) is derived from Hindu mathematics, where its use is attested already from the first centuries of our era. It must be noted moreover that the conception of zero as a number and not as a simple symbol of separation) and its introduction into calculations, also count amongst the original contribution of the Hindus." - Tradução: “... nosso sistema decimal, que (pela agência dos árabes) é derivado de matemática hindu, onde seu uso já era atestado desde os primeiros séculos da nossa era. Deve notar-se, além disso, que a concepção de zero como um número e não como um símbolo de separação simples) e a sua introdução em cálculos, também contam entre a contribuição original dos hindus.”
6. Bourbaki 1998, p. 49: Modern arithmetic was known during medieval times as "Modus Indorum" or method of the Indians. Leonardo of Pisa wrote that compared to method of the Indians all other methods is a mistake. This method of the Indians is none other than our very simple arithmetic of addition, subtraction, multiplication and division. Rules for these four simple procedures was first written down by Brahmagupta during 7th century CE. "On this point, the Hindus are already conscious of the interpretation that negative numbers must have in certain cases (a debt in a commercial problem, for instance). In the following centuries, as there is a diffusion into the West (by intermediary of the Arabs) of the methods and results of Greek and Hindu mathematics, one becomes more used to the handling of these numbers, and one begins to have other "representation" for them which are geometric or dynamic." - Tradução: “Aritmética moderna foi conhecida durante a época medieval como "Modus Indorum" ou método dos índianos. Leonardo de Pisa escreveu que, em comparação com o método dos índianos todos os outros métodos eram um erro. Este método dos índianos não é outro senão a nossa aritmética muito simples de adição, subtração, multiplicação e divisão. Regras para estes quatro procedimentos simples foram escritas pela primeira vez por Brahmagupta durante século VII d.C.. "Neste ponto, os hindus já estavam conscientes da interpretação de que os números negativos devem existir, em certos casos (a dívida em um problema comercial, por exemplo). Nos séculos seguintes, como há uma difusão para o Oeste (por intermédio dos árabes) dos métodos e resultados da matemática grega e hindu, esse sistema torna-se mais utilizado para o tratamento destes números, e começa-se a ter outra "representação" para os que eram geométricos ou dinâmicos".
7. "algebra" 2007. Britannica Concise Encyclopedia. Encyclopædia Britannica Online. 16 May 2007. Citação: "A full-fledged decimal, positional system certainly existed in India by the 9th century (CE), yet many of its central ideas had been transmitted well before that time to China and the Islamic world. Indian arithmetic, moreover, developed consistent and correct rules for operating with positive and negative numbers and for treating zero like any other number, even in problematic contexts such as division. Several hundred years passed before European mathematicians fully integrated such ideas into the developing discipline of algebra." - Tradução: “Um sistema de posicionamento decimal de pleno direito certamente existiu na Índia por volta do século IX (d.C.), mas muitas de suas idéias centrais tinham sido transmitidas bem antes que o tempo para a China e o mundo islâmico. A aritmética indiana, além disso, desenvolveu regras consistentes e corretas para operar com números positivos e negativos e para o tratamento de zero como qualquer outro número, mesmo em contextos problemáticos, como divisão. Várias centenas de anos se passaram antes de matemáticos europeus totalmente integrarem tais idéias no desenvolvimento da disciplina da álgebra.”
8. (Pingree 2003, p. 45) Citação: "Geometry, and its branch trigonometry, was the mathematics Indian astronomers used most frequently. Greek mathematicians used the full chord and never imagined the half chord that we use today. Half chord was first used by Aryabhata which made trigonometry much more simple. In fact, the Indian astronomers in the third or fourth century, using a pre-Ptolemaic Greek table of chords, produced tables of sines and versines, from which it was trivial to derive cosines. This new system of trigonometry, produced in India, was transmitted to the Arabs in the late eighth century and by them, in an expanded form, to the Latin West and the Byzantine East in the twelfth century." - Tradução: “A Geometria, e seu ramo trigonometria, era a matemática que astrônomos indianos utilizavam mais frequentemente. Matemáticos gregos usaram a corda cheia e nunca imaginaram a metade da corda que usamos hoje. A metade da corda foi usada pela primeira vez por Aryabhata que produziu trigonometria muito mais simples. Na verdade, os astrônomos indianos no terceiro ou quarto século, utilizando uma tabela pré-grega ptolomaica de cordas, produziram tabelas de senos e versenos (arco senos), a partir da qual era trivial derivar cossenos. Este novo sistema de trigonometria, produzido na Índia, foi transmitida aos árabes no final do século VIII e por elas, em uma forma expandida, para o Ocidente Latino e no Oriente Bizantino no século XII.”
9. (Bourbaki 1998, p. 126): "As for trigonometry, it is disdained by geometers and abandoned to surveyors and astronomers; it is these latter (Aristarchus, Hipparchus,Ptolemy) who establish the fundamental relations between the sides and angles of a right angled triangle (plane or spherical) and draw up the first tables (they consist of tables giving the chord of the arc cut out by an angle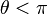 
on a circle of radius r, in other words the number 
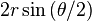; the introduction of the sine, more easily handled, is due to Hindu mathematicians of the Middle Ages)." - Tradução: “Quanto a trigonometria, é desprezada pelos geômetras e abandonada por agrimensores e astrônomos; são estes últimos (Aristarco, Hiparco, Ptolomeu) que estabelecem as relações fundamentais entre os lados e ângulos de um triângulo retângulo (plano ou esférico) e elaboram as primeiras tabelas (eles consistem de quadros com a corda do arco cortado por um ângulo 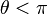sobre um círculo de raio r, em outras palavras o número 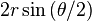; a introdução do seno, mais facilmente manipulado, é devido aos matemáticos hindus da Idade Média)."
on a circle of radius r, in other words the number ; the introduction of the sine, more easily handled, is due to Hindu mathematicians of the Middle Ages)." - Tradução: “Quanto a trigonometria, é desprezada pelos geômetras e abandonada por agrimensores e astrônomos; são estes últimos (Aristarco, Hiparco, Ptolomeu) que estabelecem as relações fundamentais entre os lados e ângulos de um triângulo retângulo (plano ou esférico) e elaboram as primeiras tabelas (eles consistem de quadros com a corda do arco cortado por um ângulo sobre um círculo de raio r, em outras palavras o número ; a introdução do seno, mais facilmente manipulado, é devido aos matemáticos hindus da Idade Média)."
10. Filliozat 2004, pp. 140–143
11. Hayashi 1995
12. Encyclopaedia Britannica (Kim Plofker) 2007, p. 6
13. Stillwell 2004, p. 173
14. Bressoud 2002, p. 12. Citação: "There is no evidence that the Indian work on series was known beyond India, or even outside Kerala, until the nineteenth century. Gold and Pingree assert [4] that by the time these series were rediscovered in Europe, they had, for all practical purposes, been lost to India. The expansions of the sine, cosine, and arc tangent had been passed down through several generations of disciples, but they remained sterile observations for which no one could find much use." - Tradução: “Não há nenhuma evidência de que o trabalho indiano sobre séries foi conhecido além da Índia, ou mesmo fora Kerala, até o século XIX. Gold e Pingree afirmam [4] que até o momento estas séries foram redescobertas na Europa, que tinham, para todos os efeitos práticos, sido perdidas para a Índia. As expansões do seno, cosseno, tangente e arco tinham sido transmitidas através de várias gerações de discípulos, mas permaneceram observações estéreis para o qual ninguém poderia encontrar muito uso.”
15. Plofker 2001, p. 293. Citação: "It is not unusual to encounter in discussions of Indian mathematics such assertions as that “the concept of differentiation was understood [in India] from the time of Manjula (... in the 10th century)” [Joseph 1991, 300], or that "we may consider Madhava to have been the founder of mathematical analysis" (Joseph 1991, 293), or that Bhaskara II may claim to be "the precursor of Newton and Leibniz in the discovery of the principle of the differential calculus" (Bag 1979, 294). ... The points of resemblance, particularly between early European calculus and the Keralese work on power series, have even inspired suggestions of a possible transmission of mathematical ideas from the Malabar coast in or after the 15th century to the Latin scholarly world (e.g., in (Bag 1979, 285)). ... It should be borne in mind, however, that such an emphasis on the similarity of Sanskrit (or Malayalam) and Latin mathematics risks diminishing our ability fully to see and comprehend the former. To speak of the Indian "discovery of the principle of the differential calculus" somewhat obscures the fact that Indian techniques for expressing changes in the Sine by means of the Cosine or vice versa, as in the examples we have seen, remained within that specific trigonometric context. The differential "principle" was not generalised to arbitrary functions—in fact, the explicit notion of an arbitrary function, not to mention that of its derivative or an algorithm for taking the derivative, is irrelevant here"
Tradução: Não é incomum encontrar em discussões de matemática indiana tais afirmações como que "o conceito de diferenciação foi entendido [na Índia] no tempo de Manjula (... no século décimo)” [Joseph 1991, 300], ou que "podemos considerar Madhava ter sido o fundador da análise matemática" (Joseph 1991, 293), ou que Bhaskara II pode ser aclamado como "o precursor de Newton e Leibniz na descoberta do princípio do cálculo diferencial" (Bag 1979, 294). … Os pontos de semelhança, particularmente entre cálculo primordial europeu e o trabalho de Keralese em séries de potências, tem sugestões inspiradas mesmo de uma possível transmissão de idéias matemáticas da costa de Malabar em ou após o século XV para o mundo acadêmico Latino (e.g., em (Bag 1979, 285)). ... Deve-se ter em mente, contudo, que tal ênfase sobre a semelhança do sânscrito (ou malaiala) e matemática latina corre o risco de diminuir a nossa capacidade plena de ver e compreender o primeiro. Para falar da "descoberta do princípio do cálculo diferencial" indiana pouco obscurece o fato de que as técnicas indianas para expressar mudanças no seno por meio da cosseno ou vice-versa, como nos exemplos que temos visto, permaneceu dentro desse específico contexto trigonométrico. O "princípio" diferencial não foi generalizado para funções arbitrárias—na verdade, a noção explícita de uma função arbitrária, para não mencionar que de uma derivada sua ou um algoritmo para tomar a derivado, é irrelevante aqui."
Tradução: Não é incomum encontrar em discussões de matemática indiana tais afirmações como que "o conceito de diferenciação foi entendido [na Índia] no tempo de Manjula (... no século décimo)” [Joseph 1991, 300], ou que "podemos considerar Madhava ter sido o fundador da análise matemática" (Joseph 1991, 293), ou que Bhaskara II pode ser aclamado como "o precursor de Newton e Leibniz na descoberta do princípio do cálculo diferencial" (Bag 1979, 294). … Os pontos de semelhança, particularmente entre cálculo primordial europeu e o trabalho de Keralese em séries de potências, tem sugestões inspiradas mesmo de uma possível transmissão de idéias matemáticas da costa de Malabar em ou após o século XV para o mundo acadêmico Latino (e.g., em (Bag 1979, 285)). ... Deve-se ter em mente, contudo, que tal ênfase sobre a semelhança do sânscrito (ou malaiala) e matemática latina corre o risco de diminuir a nossa capacidade plena de ver e compreender o primeiro. Para falar da "descoberta do princípio do cálculo diferencial" indiana pouco obscurece o fato de que as técnicas indianas para expressar mudanças no seno por meio da cosseno ou vice-versa, como nos exemplos que temos visto, permaneceu dentro desse específico contexto trigonométrico. O "princípio" diferencial não foi generalizado para funções arbitrárias—na verdade, a noção explícita de uma função arbitrária, para não mencionar que de uma derivada sua ou um algoritmo para tomar a derivado, é irrelevante aqui."
16. Pingree 1992, p. 562 Citação: "One example I can give you relates to the Indian Mādhava's demonstration, in about 1400 A.D., of the infinite power series of trigonometrical functions using geometrical and algebraic arguments. When this was first described in English by Charles Matthew Whish, in the 1830s, it was heralded as the Indians' discovery of the calculus. This claim and Mādhava's achievements were ignored by Western historians, presumably at first because they could not admit that an Indian discovered the calculus, but later because no one read anymore the Transactions of the Royal Asiatic Society, in which Whish's article was published. The matter resurfaced in the 1950s, and now we have the Sanskrit texts properly edited, and we understand the clever way that Mādhava derived the series without the calculus; but many historians still find it impossible to conceive of the problem and its solution in terms of anything other than the calculus and proclaim that the calculus is what Mādhava found. In this case the elegance and brilliance of Mādhava's mathematics are being distorted as they are buried under the current mathematical solution to a problem to which he discovered an alternate and powerful solution."
Tradução: "Um exemplo que eu posso dar-lhe relaciona-se com a demonstração do indiano Mādhava, aproximadamente em 1400 d.C.., da série de infinitas potências de funções trigonométricas usando argumentos geométricos e algébricos. Quando isso foi descrito pela primeira vez em Inglês por Charles Matthew Whish, nos anos 1830s, foi anunciado como a descoberta do cálculo dos indianos. Esta alegação e conquistas de Mādhava foram ignoradas pelos historiadores ocidentais, presumivelmente, em primeiro lugar porque não podiam admitir que um indiano descobriu o cálculo, mas mais tarde, porque ninguém mais leria as Transactions of the Royal Asiatic Society, na qual o artigo de Whish foi publicado. A questão ressurgiu na década de 1950, e agora temos os textos sânscritos devidamente editados, e entendemos a maneira inteligente que Mādhava derivou a série sem o cálculo; mas muitos historiadores ainda acham que é impossível conceber o problema e sua solução em termos de outra coisa senão o cálculo e proclamar que o cálculo é o que Mādhava encontrou. Neste caso, a elegância e o brilho da matemática de Mādhava estão sendo distorcidos como eles estão enterrados sob a solução matemática atual para um problema para o qual ele descobriu uma alternativa e uma solução poderosa."
Tradução: "Um exemplo que eu posso dar-lhe relaciona-se com a demonstração do indiano Mādhava, aproximadamente em 1400 d.C.., da série de infinitas potências de funções trigonométricas usando argumentos geométricos e algébricos. Quando isso foi descrito pela primeira vez em Inglês por Charles Matthew Whish, nos anos 1830s, foi anunciado como a descoberta do cálculo dos indianos. Esta alegação e conquistas de Mādhava foram ignoradas pelos historiadores ocidentais, presumivelmente, em primeiro lugar porque não podiam admitir que um indiano descobriu o cálculo, mas mais tarde, porque ninguém mais leria as Transactions of the Royal Asiatic Society, na qual o artigo de Whish foi publicado. A questão ressurgiu na década de 1950, e agora temos os textos sânscritos devidamente editados, e entendemos a maneira inteligente que Mādhava derivou a série sem o cálculo; mas muitos historiadores ainda acham que é impossível conceber o problema e sua solução em termos de outra coisa senão o cálculo e proclamar que o cálculo é o que Mādhava encontrou. Neste caso, a elegância e o brilho da matemática de Mādhava estão sendo distorcidos como eles estão enterrados sob a solução matemática atual para um problema para o qual ele descobriu uma alternativa e uma solução poderosa."
17. Katz 1995, pp. 173–174 Citação: "How close did Islamic and Indian scholars come to inventing the calculus? Islamic scholars nearly developed a general formula for finding integrals of polynomials by A.D. 1000—and evidently could find such a formula for any polynomial in which they were interested. But, it appears, they were not interested in any polynomial of degree higher than four, at least in any of the material that has come down to us. Indian scholars, on the other hand, were by 1600 able to use ibn al-Haytham's sum formula for arbitrary integral powers in calculating power series for the functions in which they were interested. By the same time, they also knew how to calculate the differentials of these functions. So some of the basic ideas of calculus were known in Egypt and India many centuries before Newton. It does not appear, however, that either Islamic or Indian mathematicians saw the necessity of connecting some of the disparate ideas that we include under the name calculus. They were apparently only interested in specific cases in which these ideas were needed.
There is no danger, therefore, that we will have to rewrite the history texts to remove the statement that Newton and Leibniz invented the calculus. They were certainly the ones who were able to combine many differing ideas under the two unifying themes of the derivative and the integral, show the connection between them, and turn the calculus into the great problem-solving tool we have today."
Tradução: "Quão perto estudiosos islâmicos e indianos estiveram de inventar o cálculo? Estudiosos islâmicos quase desenvolveram uma fórmula geral para a determinação de integrais de polinômios em 1000 d.C.—e, evidentemente, poderiam encontrar uma fórmula para qualquer polinômio em que eles estavam interessados. Mas, ao que parece, eles não estavam interessados em qualquer polinômio de grau maior do que quatro, pelo menos, em qualquer parte do material que chegou até nós. Estudiosos indianos, por outro lado, eram em 1600 capazes de usar a fórmula da soma de Ibn al-Haytham para potências arbitrárias integrais no cálculo de séries de potências para as funções em que estavam interessados. Ao mesmo tempo, eles também sabiam como calcular as diferenciais destas funções. Assim, algumas das idéias básicas de cálculo eram conhecidas no Egito e Índia muitos séculos antes de Newton. Não parece, no entanto, que os matemáticos islâmicos ou indianos viram a necessidade de ligar algumas das ideias díspares que incluímos sob o nome de cálculo. Eles estavam aparentemente interessados apenas em casos específicos nos quais essas ideias eram necessárias.
Não há perigo, portanto, que tenhamos de reescrever os textos de história para remover a afirmação de que Newton e Leibniz tenham inventado o cálculo. Eles foram certamente os únicos que foram capazes de combinar muitas idéias diferentes ao abrigo dos dois temas unificadores da derivada e a integral, mostrando a conexão entre eles, e tornar o cálculo a grande ferramenta de resolução de problemas que temos hoje."
18. Sergent, Bernard (1997), Genèse de l'Inde (em francês), Paris: Payot, p. 113, ISBN 2-228-89116-9
19. Coppa, A. et al. (6 April 2006), "Early Neolithic tradition of dentistry: Flint tips were surprisingly effective for drilling tooth enamel in a prehistoric population" (PDF), Nature 440 (7085): 755–6, doi:10.1038/440755a, PMID 16598247.
20. Bisht, R. S. (1982), "Excavations at Banawali: 1974–77", in Possehl, Gregory L. (ed.), Harappan Civilisation: A Contemporary Perspective, New Delhi: Oxford and IBH Publishing Co., pp. 113–124
21. A. Seidenberg, 1978. The origin of mathematics. Archive for the history of Exact Sciences, vol 18.
22. (Staal 1999)
23. (Hayashi 2003, p. 118)
24. (Hayashi 2005, p. 363)
25. Trios pitagóricos são trios de inteiros (a, b, c) com a propriedade: a2+b2 = c2. Então, 32+42 = 52, 82+152 = 172,122+352 = 372, etc.
26. (Cooke 2005, p. 198): "The arithmetic content of the Śulva Sūtras consists of rules for finding Pythagorean triples such as (3, 4, 5), (5, 12, 13), (8, 15, 17), and(12, 35, 37). It is not certain what practical use these arithmetic rules had. The best conjecture is that they were part of religious ritual. A Hindu home was required to have three fires burning at three different altars. The three altars were to be of different shapes, but all three were to have the same area. These conditions led to certain "Diophantine" problems, a particular case of which is the generation of Pythagorean triples, so as to make one square integer equal to the sum of two others." - Tradução: “O conteúdo aritmético dos Śulva Sūtras consiste em regras para encontrar triplos potagóricos, tais como (3, 4, 5), (5, 12, 13), (8, 15, 17), e (12, 35, 37). Não é certo qual utilização prática essas regras aritméticas tinham. A melhor conjectura é que eles eram parte de um ritual religioso. Uma casa Hindu era obrigada a ter três piras cerimoniais que queimavam em três altares diferentes. Os três altares eram para ser de formas diferentes, mas todos os três eram para ter a mesma área. Estas condições originaram alguns problemas "Diofantinos", caso particular dos quais é a geração de trios pitagóricos, de modo a fazer um número inteiro quadrado igual à soma dos outros dois.”
27. (Cooke 2005, pp. 199–200): "The requirement of three altars of equal areas but different shapes would explain the interest in transformation of areas. Among other transformation of area problems the Hindus considered in particular the problem of squaring the circle. The Bodhayana Sutra states the converse problem of constructing a circle equal to a given square. The following approximate construction is given as the solution.... this result is only approximate. The authors, however, made no distinction between the two results. In terms that we can appreciate, this construction gives a value for π of 18 (3 − 2√2), which is about 3.088." - Tradução: “A exigência de três altares de áreas iguais, mas diferentes formas, explicaria o interesse na transformação de áreas. Entre outras transformações de problemas da área os Hindus consideravam, em particular, o problema da quadratura do círculo. O Bodhayana Sutra declara o problema inverso de construção de um círculo de área igual a um determinado quadrado (“circulatura” do quadrado). A construção seguinte aproximada é dada como a solução .... este resultado é apenas aproximado. Os autores, no entanto, não fazem distinção entre os dois resultados. Em termos que podemos apreciar, esta construção dá um valor para π de 18 (3 − 2√2), o que é cerca de 3.088."
28. (Joseph 2000, p. 229)
29. (Cooke 2005, p. 200)
30. O valor dessa aproximação, 577/408, é o sétimo de uma sequência de aproximações cada vez mais precisas, 3/2, 7/5, 17/12, ... a √2, numeradores e denominadores os quais eram conhecidos como "números laterais e diãmetros" para os gregos antigos, e na matemática moderna são chamados os números de Pell. Se x/y é um termo nessa sequência de aproximações, o próximo é (x + 2y)/(x + y). Estas aproximações podem também ser obtidas por truncagem da representação da fração contínua √2.
31. Neugebauer, O. and A. Sachs. 1945. Mathematical Cuneiform Texts, New Haven, CT, Yale University Press. p. 45.
33. Três inteiros positivos 
formam um trio pitagórico primitivo se 
e se o mais alto fator comum de 
é 1 (são “primos entre si”). No exemplo particular do documento Plimpton 322, isso significa que 
e que os três números não têm quaisquer fatores comuns. No entanto, alguns estudiosos têm contestado a interpretação pitagoreana desta tábula; ver Plimpton 322 para detalhes.
formam um trio pitagórico primitivo se 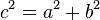e se o mais alto fator comum de 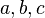é 1 (são “primos entre si”). No exemplo particular do documento Plimpton 322, isso significa que 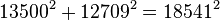e que os três números não têm quaisquer fatores comuns. No entanto, alguns estudiosos têm contestado a interpretação pitagoreana desta tábula; ver Plimpton 322 para detalhes.
34. (Dani 2003)
36. (Singh 1936, pp. 623–624)
37. (Filliozat 2004, p. 137)
38. (Pingree 1988, p. 637)
39. (Staal 1986)
40. (Filliozat 2004, p. 139)
41. (Filliozat 2004, pp. 140–141)
42. (Yano 2006, p. 146)
43. (Filliozat 2004, pp. 143–144)
44. (Pingree 1988, p. 638)
45. (Hayashi 2003, pp. 122–123)
46. (Hayashi 2003, p. 119)
47. Plofker 2007, p. 395
48. Plofker 2007, p. 395, Plofker 2009, pp. 47–48
49. (Hayashi 2005, p. 366)
50. Plofker 2009, p. 45
51. Plofker 2009, p. 46
52. Plofker 2009, p. 47
53. (Pingree 1978, p. 494)
54. Plofker 2009, p. 48
55. (Hayashi 2005, p. 371)
56. (Datta 1931, p. 566)
57. (Ifrah 2000, p. 464) Citação: "To give the second or fourth century CE as the date of this document would be an evident contradiction; it would mean that a northern derivative of Gupta writing had been developed two or three centuries before the Gupta writing itself appeared. Guptaonly began to evolve into Shāradā style around the ninth century CE. In other words, the Bak(h)shali manuscript cannot have been written earlier than the ninth century CE. However, in the light of certain characteristic indications, it could not have been written any later than the twelfth century CE." - Tradução: “Afirmar o segundo ou quarto século d.C. como a data deste documento seria uma contradição evidente; isso significaria que um derivado da escrita do norte de Gupta foi desenvolvida dois ou três séculos antes da escrita Gupta aparecer. Gupta somente começou a evoluir em estilo Shāradā por volta do século IX d.C.. Em outras palavras, o manuscrito Bak(h)shali pode não ter sido escrito antes do século IX d.C.. No entanto, à luz de certas indicações características, não poderia ter sido escrito mais tarde do que o século XII d.C.."
58. (Hayashi 2005, p. 371) Citação:"The dates so far proposed for the Bakhshali work vary from the third to the twelfth centuries CE, but a recently made comparative study has shown many similarities, particularly in the style of exposition and terminology, between Bakhshalī work and Bhāskara I's commentary on the Āryabhatīya. This seems to indicate that both works belong to nearly the same period, although this does not deny the possibility that some of the rules and examples in the Bakhshālī work date from anterior periods." - Tradução: “As datas até agora propostas para o trabalho Bakhshali varian a partir do terceiro ao décimo segundo séculos d.C., mas um estudo comparativo feito recentemente mostrou muitas semelhanças, principalmente no estilo de exposição e terminologia, entre o trabalho Bakhshalī e comentários de Bhaskara I no Āryabhatīya. Isto parece indicar que ambas as obras pertencem quase ao mesmo período, embora isso não nega a possibilidade de que algumas das regras e exemplos na data do trabalho Bakhshālī sejam de períodos anteriores.
59. (Ifrah 2000, p. 464)
60. Anton, Howard and Chris Rorres. 2005. Elementary Linear Algebra with Applications. 9th edition. New York: John Wiley and Sons. 864 pages. ISBN 0-471-66959-8.
61. (Neugebauer & Pingree (eds.) 1970)
62. Cooke, Roger (1997), "The Mathematics of the Hindus",The History of Mathematics: A Brief Course, Wiley-Interscience, p. 197, ISBN 0-471-18082-3, A palavra Siddhanta significa aquilo o que está provado ou estabelecido. Os Sulva Sutras são de origem Hindu, mas o Siddhantas contem muitas palavras de origem estrangeira que, sem dúvida, têm raízes na Mesopotâmia e na Grécia.
63. Katz, Victor J. (1995), "Ideas of Calculus in Islam and India", Mathematics Magazine 68 (3): 163–174,doi:10.2307/2691411.
64. (Hayashi 2005, p. 369)
65. (Hayashi 2003, pp. 121–122)
66. (Stillwell 2004, p. 77)
67. (Stillwell 2004, p. 87)
68. (Stillwell 2004, pp. 72–73)
69. (Stillwell 2004, pp. 74–76)
70. Gupta, R. C. (2000), "History of Mathematics in India", in Hoiberg, Dale; Ramchandani, Indu, Students' Britannica India: Select essays, Popular Prakashan, p. 329
72. Joseph (2000), p. 298–300.
73. (Roy 1990)
74. (Bressoud 2002)
75. (Katz 1995)
76. Singh, A. N. Singh (1936), "On the Use of Series in Hindu Mathematics", Osiris 1: 606–628,doi:10.1086/368443.
77. Edwards, C. H., Jr. 1979. The Historical Development of the Calculus. New York: Springer-Verlag.
78. (Whish 1835)
79. Rajagopal, C.; Rangachari, M. S. (1949), "A Neglected Chapter of Hindu Mathematics", Scripta Mathematica 15: 201–209.
80. Rajagopal, C.; Rangachari, M. S. (1951), "On the Hindu proof of Gregory's series", Ibid. 17: 65–74.
81. Rajagopal, C.; Venkataraman, A. (1949), "The sine and cosine power series in Hindu mathematics", Journal of the Royal Asiatic Society of Bengal (Science) 15: 1–13.
82. Rajagopal, C.; Rangachari, M. S. (1977), "On an untapped source of medieval Keralese mathematics",Archive for the History of Exact Sciences 18: 89–102.
83. Rajagopal, C.; Rangachari, M. S. (1986), "On Medieval Kerala Mathematics", Archive for the History of Exact Sciences 35 (2): 91–99, doi:10.1007/BF00357622.
84. Joseph, G. G. 1997. "Foundations of Eurocentrism in Mathematics." In Ethnomathematics: Challenging Eurocentrism in Mathematics Education (Eds. Powell, A. B. et al.). SUNY Press. ISBN 0-7914-3352-8. p.67-68.
85. Cajori, Florian (1893), "The Hindoos", A History of Mathematics P 86, Macmillan & Co., Citação: “In algebra, there was probably a mutual giving and receiving [between Greece and India]. We suspect that Diophantus got his first glimpse of algebraic knowledge from India.” - Tradução: “Em álgebra, houve provavelmente uma doação e recebimento recíproco [entre a Grécia e a Índia]. Suspeitamos que Diofanto conseguiu seu primeiro vislumbre de conhecimento algébrico da Índia.”
86. Florian Cajori (2010). "A History of Elementary Mathematics – With Hints on Methods of Teaching". p.94. ISBN 1-4460-2221-8
87. Almeida, D. F.; John, J. K.; Zadorozhnyy, A. (2001), "Keralese Mathematics: Its Possible Transmission to Europe and the Consequential Educational Implications",Journal of Natural Geometry 20: 77–104.
88. Gold, D.; Pingree, D. (1991), "A hitherto unknown Sanskrit work concerning Madhava's derivation of the power series for sine and cosine", Historia Scientiarum 42: 49–65.
Postagens
Nenhum comentário:
Postar um comentário