Gripe Mexicana

Os recentes acontecimentos já eram mais que esperados.

Há anos os infectologistas e epidemiologistas esperavam que surgisse uma mutação no vírus influenza que causasse uma infecção (logo, uma epidemia) perigosa ao ser humano.

O vírus influenza é natural nas aves domésticas, em especial dos patos asiáticos, e seguidamente, e até podemos dizer uma vez por ano, muta para os porcos, e destes para o homem com ainda mais facilidade.

Tal acontece em média uma vez por ano. Exatamente por tal motivo nos vacinamos (em especial idosos e crianças) uma vez por ano, quando nos tornamos relativamente imunes (ou seja, nossos anticorpos ficam disponíveis, preparados) a última variedade do vírus (pelo menos, a que conseguimos isolar).

O vírus influenza (http://www.bma.org.uk/)

As vezes a mutação é ruim para o vírus, logo, pouco maligna para nós. As vezes não, e aí que reside o problema. Estatisticamente, e até podemos dizer probabilisticamente, e façamos uma analogia com um dado, exemplo mais simples de se entender probabilidades, cai 4, 5 ou 6, e temos o jogo ganho, e o vírus nos dá apenas uma febrezinha, e parcela da população nem sequer tem mais que um desconforto.

Mas as vezes cai no dado 3, 2 ou 1. E aí reside o problema. Nestas jogadas, perdemos o jogo.

A última vez que caiu, digamos 1, foi durante a "febre espanhola" (ou "gripe espanhola"), de 1918-1919, com uma taxa de letalidade de 6 a 8 % na sua fase mais maligna.

Foi o que chamamos de pandemia, afetando todo a humanidade, em praticamente todos os pontos da Terra. Atingiu especialmente os jovens. Calcula-se que tenha atingido 50% da população mundial, tendo matado de 20 a 40 milhões de pessoas, sendo considerada o fenômeno epidêmico de todos os tempos. Suas mortes registradas superaram as da Primeira Guerra Mundial (19 a 20 milhões estimados). Mas não se conhece o verdadeiro total, pela falta de estatísticas confiáveis, principalmente na China e Índia, que podem esconder um número ainda maior de vítimas.

Foi tão evastadora que não poupou classes sociais ou posições de poder (a peste negra, em comparação, matava mais a população pobre e "servil", pela presença e proximidade de ratos), a tal ponto que o presidente do Brasil, Rodrigues Alves, foi uma de suas notórias vítimas.


Sabemos que vírus mutam, e comparamos tais mutações a dados, mas temos de entender porque que mais cedo ou mais tarde, somos castigados com um resultado 1.


Probabilidades e Distribuição de Poisson


Quando lançamos um dado, logicamente de seis dados, a probabilidade de cair qualquer de seus dados é UMA em SEIS, ou 1/6, como nos habituamos a tratar em matemática.

Uma pergunta adequada a ter esta resposta seria:

Qual a probabilidade de em UM lançamento, termos o resultado 1 em um dado?

Mas quando perguntamos:

Qual a probabilidade de em UM MILHÃO de lançamentos, termos UM resultado 1 pelo menos em um dado?

A resposta não será 1/6, pois esta é a resposta de aproximadamente em quantos destes um milhão de lançamentos cairá o resultado 1 (aproximadamente 166666 vezes).

A probabilidade de cair um dado PELO MENOS com o resultado 1 em um milhão de lançamentos é de um número que TENDE a 1, e podemos dizer com segurança, por um caminho mais de "juízo" que matemático, que sabemos que certamente, ao se lançar um dado durante um milhão de vezes, teremos pelo menos um resultado igual a 1.

Em outras palavras, por um caminho inverso, é praticamente impossível em um milhão de lançamentos, que não caia 1.

A distribuição que trata deste tipo de problema em probabilidades é chamada de distribuição de Poisson. Ela trata de probabilidades que sejam "acumulativas" (notemos as aspas, pois não trata-se de uma simples soma). Quanto mais tempo (ou lançamentos) passa, mais provável ocorrer aquele evento esperado, ainda que em cada lançamento, a probabilidade do resultado 1 seja 1/6, mas se ele "até agora não ocorreu", certamente ocorrerá no futuro, ou AGORA.

Exatamente por estas questões, que a MEGASENA acumula, mas não acumula eternamente, pois mais cedo ou mais tarde, e podemos afirmar um limite até hoje de mais ou menos 9 semanas, alguém é o feliz ganhador de uma "bolada".

A curva de uma distribuição acumulada nos dá a idéia mais clara do que tratamos: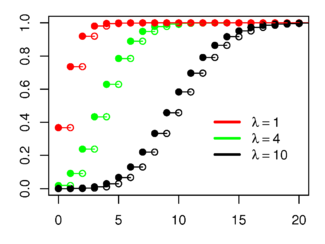

(Grato à Wiki-en!)
Como dizia um ex-professor de Álgebra Linear e Geometria Analítica: -Não sei se me fiz claro?

Para um entendimento mais formal do que apresentei, recomendo a leitura do bem claro e simples artigo da Wiki-pt:

http://pt.wikipedia.org/wiki/Distribui%C3%A7%C3%A3o_de_Poisson

Assim, dentro da questão que estamos tratando, vírus mutam aleatoriamente, e neste aleatoriamente, mais cedo ou mais tarde, mutam sendo danosos ao extremo ao ser humano.

Assim, se esta atual epidemia não se tornar uma pandemia, mais cedo ou mais tarde, tal como é certo que quando jogamos dados tiramos o mais baixo valor, os vírus mutarão para uma epidemia mais grave, e talvez, uma pandemia.

Assim, temos de estar preparados. Mas será que estamos?___________________________________________

A seguir:

Medicação e tratamentos

Medidas pessoais

Medidas governamentais

A questão populacional